题目内容
15．设集合A={-1，1，2}，B={a+1，a2-2}，若A∩B={-1，2}，则a的值为（ ）| A． | -2或1 | B． | 0或1 | C． | -2或-1 | D． | 0或-2 |
分析 由交集定义得到$\left\{\begin{array}{l}{a+1=-1}\\{{a}^{2}-2=2}\end{array}\right.$或$\left\{\begin{array}{l}{a+1=2}\\{{a}^{2}-2=-1}\end{array}\right.$，由此能求出a的值．
解答 解：∵集合A={-1，1，2}，B={a+1，a2-2}，A∩B={-1，2}，
∴$\left\{\begin{array}{l}{a+1=-1}\\{{a}^{2}-2=2}\end{array}\right.$或$\left\{\begin{array}{l}{a+1=2}\\{{a}^{2}-2=-1}\end{array}\right.$，
解得a=-2或a=1．
故选：A．
点评 本题考查a的值的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
6．若直线y=3x与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）有公共点，则双曲线的离心率的取值范围为（ ）
| A． | $（1，\sqrt{10}）$ | B． | $（\sqrt{10}，+∞）$ | C． | $（{1，\sqrt{10}}]$ | D． | $[{\sqrt{10}}\right.，+∞）$ |
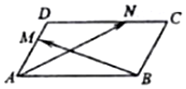如图，在平行四边形ABCD中，∠BAD=$\frac{π}{3}$，AB=2，AD=1，若M、N分别是边AD、CD上的点，且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ，其中λ∈[0，1]，则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是（ ）
某水泥厂销售工作人员根据以往该厂的销售情况，绘制了该厂日销售量的频率分布直方图，如图所示：将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．