已知i为虚数单位.复数z满足2.则|z|为( )A．$\sqrt{2}$B．1C．$\frac{1}{2}$D．$\frac{{\sqrt{2}}}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

10．已知i为虚数单位，复数z满足（1+i）z=（1-i）²，则|z|为（　　）

A．

$\sqrt{2}$

B．

C．

$\frac{1}{2}$

D．

$\frac{{\sqrt{2}}}{2}$

分析利用复数的运算法则、共轭复数的定义、模的计算公式即可得出．

解答解：（1+i）z=（1-i）²，∴（1-i）（1+i）z=-2i（1-i），2z=-2-2i，即z=1-i．
则|z|=$\sqrt{{1}^{2}+（-1）^{2}}$=$\sqrt{2}$．
故选：A．

点评本题考查了复数的运算法则、共轭复数的定义、模的计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案

学而优中考专题分类集训南京大学出版社系列答案

相关题目

20．

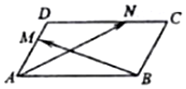如图，在平行四边形ABCD中，∠BAD=$\frac{π}{3}$，AB=2，AD=1，若M、N分别是边AD、CD上的点，且满足$\frac{MD}{AD}$=$\frac{NC}{DC}$=λ，其中λ∈[0，1]，则$\overrightarrow{AN}$•$\overrightarrow{BM}$的取值范围是（　　）

1．一个三角形可分为以内切圆半径为高，以原三角形三条边为底的三个三角形，类比此方法，若一个三棱锥的体积V=2，表面积S=3，则该三棱锥内切球的体积为（　　）

18．已知菱形ABCD的边长为2，E为AB的中点，∠ABC=120°，则$\overrightarrow{DE}$•$\overrightarrow{BD}$的值为（　　）

5．α，β为两个不同的平面，m，n为两条不同的直线，下列命题中正确的是①④（填上所有正确命题的序号）．
①若α∥β，m?α，则m∥β；
②若m∥α，n?α，则m∥n；
③若α⊥β，α∩β=n，m⊥n，则m⊥β；
④若n⊥α，n⊥β，m⊥α，则m⊥β．

15．${（\frac{5}{{\sqrt{x}}}-x）^m}$的展开式中各项系数的和为256，则该展开式的二项式系数的最大值为6．

2．已知函数$f（x）=\frac{1}{3}{x^3}-\frac{a+1}{2}{x^2}+ax-1$，$g（x）=\frac{1}{2}（a-4）{x^2}$，其中a≥1．
（Ⅰ）f（x）在（0，2）上的值域为（s，t），求a的取值范围；
（Ⅱ）若a≥3，对于区间[2，3]上的任意两个不相等的实数x₁、x₂，都有|f（x₁）-f（x₂）|＞|g（x₁）-g（x₂）|成立，求实数a的取值范围．

19．已知数列{a_n}中，a₁=2，a₂=4，设S_n为数列{a_n}的前n项和，对于任意的n＞1，n∈N^*，S_n+1+S_n-1=2（S_n+1）．
（1）求数列{a_n}的通项公式；
（2）设b_n=$\frac{n}{{2}^{{a}_{n}}}$，求{b_n}的前n项和T_n．

20．如图程序框图，输出a的结果为（　　）

	A．	初始值a		B．	三个数中的最大值
	C．	三个数中的最小值		D．	初始值c

试题分类