题目内容

8．已知函数f（x）=asinx+btanx+|x|，满足f（5）=7，则f（-5）=3．

分析 根据函数奇偶性的性质，利用整体代换的思想进行求解即可．

解答 解：∵f（x）=asinx+btanx+|x|，
∴f（5）=asin5+btan5+5=7，
即asin5+btan5=2，
则f（-5）=-asin5-btan5+5=-（asin5+btan5）+5=-2+5=3，
故答案为：3．

点评 本题主要考查函数值的计算，根据函数奇偶性的性质，利用方程组思想是解决本题的关键．

练习册系列答案
相关题目
18．把二进制数11000转换为十进制数，该十进制数为（　　）
A．48B．24C．12D．6
19．已知$cos（\frac{π}{4}-α）=\frac{4}{5}$，则$sin（\frac{π}{4}+α）$=（　　）
A．$\frac{4}{5}$B．$\frac{3}{5}$C．$-\frac{4}{5}$D．$-\frac{3}{5}$
16．设函数f（x）为奇函数，且在（-∞，0）上是减函数，若f（-3）=0，则xf（x）＜0的解集为（　　）
A．（-3，0）∪（3，+∞）B．（-∞，-3）∪（0，3）C．（-∞，-3）∪（3，+∞）D．（-3，0）∪（0，3）
3．设变量x，y满足约束条件$\left\{\begin{array}{l}x+y-2≤0\\ x-y+2≥0\\ y≥0\end{array}\right.$，则目标函数z=x+2y的最小值为-2．
13．A为三角形一内角，若sinA+cosA=$\frac{1}{5}$，cosA-sinA=-$\frac{7}{5}$．
20．曲线y=sinx（0≤x≤π）与直线$y=\frac{1}{2}$围成的封闭图形的面积是$\sqrt{3}$-$\frac{π}{3}$．
17．函数f（x）=sin（2x-$\frac{π}{3}$）（x∈R）的图象为C，以下结论正确的是①②．（写出所有正确结论的编号）
①图象C关于直线x=$\frac{11π}{12}$对称；
②图象C关于点（$\frac{2π}{3}$，0）对称；
③函数f（x）在区间（-$\frac{π}{12}$，$\frac{5π}{2}$）内是增函数；
④由y=sin2x的图象向右平移$\frac{π}{3}$个单位长度可以得到图象C．
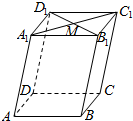18．如图，已知平行六面体ABCD-A1B1C1D1，M为A1C1与B1D1的交点，化简下列向量表达式：
（1）$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$；
（2）$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{A{{\;}_{1}D}_{1}}$；
（3）$\overrightarrow{A{A}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{B}_{1}}$+$\frac{1}{2}$$\overrightarrow{{A}_{1}{D}_{1}}$；
（4）$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$+$\overrightarrow{{C}_{1}{A}_{1}}$+$\overrightarrow{{A}_{1}A}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网