题目内容
3．设变量x，y满足约束条件$\left\{\begin{array}{l}x+y-2≤0\\ x-y+2≥0\\ y≥0\end{array}\right.$，则目标函数z=x+2y的最小值为-2．分析 先画出满足条件的平面区域，结合函数的图象求出直线y=-$\frac{1}{2}$x+$\frac{z}{2}$过A（-2，0）时，z最小，求出z的最小值即可．
解答 解：画出满足条件的平面区域，如图示：
，
由z=x+2y得：y=-$\frac{1}{2}$x+$\frac{z}{2}$，
∴y=-$\frac{1}{2}$x+$\frac{z}{2}$过A（-2，0）时，z最小，
z的最小值是-2，
故答案为：-2．
点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道基础题．
练习册系列答案
相关题目
13．体积为$\frac{4}{3}π$的球O放置在棱长为4的正方体ABCD-A1B1C1D1上，且与上表面A1B1C1D1相切，切点为该表面的中心，则四棱锥O-ABCD的外接球的半径为（ ）
| A． | $\frac{10}{3}$ | B． | $\frac{33}{10}$ | C． | $\frac{23}{6}$ | D． | $\frac{41}{12}$ |
18．在区间（0，1）内任取两个数x，y，则满足y≥2x概率是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
12．等腰梯形ABCD，上底CD=1，腰AD=CB=$\sqrt{2}$，下底AB=3，以下底所在直线为x轴，则由斜二侧画法画出的直观图A′B′C′D′的面积为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{{\sqrt{2}}}{4}$ | D． | 2 |
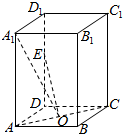如图所示，在长方体体ABCD-A1B1C1D1中，O为AC的中点．