Question

已知椭圆C中心是坐标原点O，焦点在x轴上，离心率e=

3

2

，P（1，

3

2

）为椭圆上的一点．
（1）求椭圆C的标准方程；
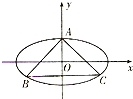
（2）如图，记椭圆C的上顶点为A，问是否存在这样的以A为直角顶点的内接与椭圆的等腰直角△ABC，若存在，共有几个？若不存在，请说明理由．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）设椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0），利用离心率e=

3

2

，P（1，

3

2

）为椭圆上的一点，建立方程，即可求出椭圆C的标准方程；
（2）设直线AB：y=kx+1，代入椭圆方程，求出|AB|，|AC|，利用|AB|=|AC|，建立方程，即可求得结论．

解答： 解：（1）设椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）．
∵离心率e=

3

2

，P（1，

3

2

）为椭圆上的一点，
∴

c

a

=

3

2

，

1

a2

+

3 4

b2

=1
解得a²=4，b²=1，c=

3

．
∴椭圆的标准方程为

x2

4

+y2=1；
（2）由题意A（0，1），直线AB，AC的斜率存在且不为0，设k_AB=k＞0，则k_AC=-

1

k

，
设B（x₁，y₁），C（x₂，y₂），直线AB：y=kx+1，
代入椭圆方程可得（1+4k²）x²+8kx=0，∴x₁=-

8k

1+4k2

，
|AB|=

1+k2

|x₁|=

1+k2

•

8k

1+4k2

，
同理|AC|=

8 1+k2

k2+4

，
若|AB|=|AC|，则

1+k2

•

8k

1+4k2

=

8 1+k2

k2+4

，
∴（k-1）（k²-3k+1）=0，
∴k=1或

3± 5

2

，
∴存在3个以A为直角顶点的内接与椭圆的等腰直角△ABC．

点评：熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立是解题的关键．