题目内容
求满足下列条件的直线的方程.
(Ⅰ)经过点B(3,0),且与直线2x+y-5=0垂直;
(Ⅱ)经过两直线2x+y-8=0和x-2y+1=0的交点,且平行于直线4x-3y-7=0.
(Ⅰ)经过点B(3,0),且与直线2x+y-5=0垂直;
(Ⅱ)经过两直线2x+y-8=0和x-2y+1=0的交点,且平行于直线4x-3y-7=0.
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(I)由垂直关系可得所求直线的斜率为k,可得点斜式方程,化为一般式可得;
(II)联立方程组
,解方程组可得交点坐标,由平行关系可得直线的斜率,可得点斜式方程,化为一般式可得.
(II)联立方程组
|
解答:
解:(I)∵直线2x+y-5=0的斜率为-2,
由垂直关系可得所求直线的斜率为k=
,
∴由点斜式得y=
(x-3),
化为一般式可得x-2y-3=0;
(II)联立方程组
,解得
,
即两直线2x+y-8=0和x-2y+1=0的交点为(3,2)
∴所求直线方程为y-2=
(x-3),
化为一般式可得4x-3y-6=0
由垂直关系可得所求直线的斜率为k=
| 1 |
| 2 |
∴由点斜式得y=
| 1 |
| 2 |
化为一般式可得x-2y-3=0;
(II)联立方程组
|
|
即两直线2x+y-8=0和x-2y+1=0的交点为(3,2)
∴所求直线方程为y-2=
| 4 |
| 3 |
化为一般式可得4x-3y-6=0
点评:本题考查直线的一般式方程与直线的平行和垂直关系,属基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )| A、4320 | B、2880 |
| C、8640 | D、2160 |
在关于x的方程x2-ax+4=0,x2+(a-1)x+16=0,x2+2ax+3a+10=0中,已知至少有一个方程有实数根,则实数a的取值范围为( )
| A、-4≤a≤4 |
| B、a≥9或a≤-7 |
| C、a≤-2或a≥4 |
| D、-2<a<4 |
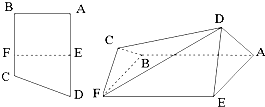 如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.
如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.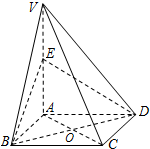 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.