题目内容
过点P（-1，4）作圆x2+y2-4x-6y+12=0的切线，则切线长为（ ）
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |
考点：圆的切线方程
专题：直线与圆
分析：把圆的一般方程化为标准方程，求出圆心到点P的距离d，根据圆的半径r，即可求出切线长l．
解答：
解：∵圆x2+y2-4x-6y+12=0的标准方程是
（x-2）2+（x-3）2=1，
∴圆心（2，3）到点P的距离是
d=
=
；
圆的半径r=1，
∴切线长为
l=
=
=3．
故选：A．
（x-2）2+（x-3）2=1，
∴圆心（2，3）到点P的距离是
d=
| (2+1)2+(3-4)2 |
| 10 |
圆的半径r=1，
∴切线长为
l=
| d2-r2 |
(
|
故选：A．
点评：本题考查了直线与圆的应用问题，解题时应熟练地掌握圆的标准方程与一般方程的互化问题，是基础题．
练习册系列答案
相关题目
已知圆（x-a）2+（y-b）2=1与二直线l1：3x-4y-1=0和l2：4x+3y+1=0都有公共点，则
的取值范围为（ ）
| b |
| a-2 |
A、[-
| ||||
B、[
| ||||
C、（-∞，-
| ||||
D、[-
|
已知直线m，n和平面α，满足m?α，n∥α，则直线m，n的关系是（ ）
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
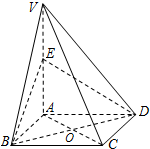如图，在四棱锥V-ABCD中，底面ABCD是正方形，侧棱VA⊥底面ABCD，点E为VA的中点．