题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(x+2),}&{x≥2}\\{{2}^{1-x},}&{x<2}\end{array}\right.$(a>0且a≠1),若f(6)+f(-1)=7,函数y=f(x)-b仅有一个零点,则实数b的取值范围为( )| A. | [$\frac{1}{2}$,2] | B. | ($\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,2) | D. | ($\frac{1}{2}$,2) |
分析 由已知函数解析式结合f(6)+f(-1)=7求得a值,把函数y=f(x)-b仅有一个零点,即y=f(x)与y=b的图象只有一个交点,作出函数图象,数形结合得答案.
解答 解:∵f(6)+f(-1)=7,∴loga8+4=7,即loga8=3,∴a=2.
则$f(x)=\left\{\begin{array}{l}{lo{g}_{2}(x+2),x≥2}\\{{2}^{1-x},x<2}\end{array}\right.$,
函数y=f(x)-b仅有一个零点,即y=f(x)与y=b的图象只有一个交点.
作出函数图象如图:
由图象可得,实数b的取值范围为:($\frac{1}{2}$,2).
故选:D.
点评 本题考查函数零点的判定定理,考查数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
13.已知正项等差数列{an}的前n项和为Sn,S10=40,则a3•a8的最大值为( )
| A. | 14 | B. | 16 | C. | 24 | D. | 40 |
14.下列函数中既是偶函数,又在区间(0,1)上单调递增的是( )
| A. | y=cosx | B. | $y={x^{\frac{1}{2}}}$ | C. | y=2|x| | D. | y=|lgx| |
11.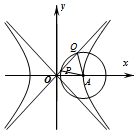 如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )
 如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$,且$|{\overrightarrow{OQ}}|=3|{\overrightarrow{OP}}$|,则双曲线C的离心率为( )| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
18. 某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
 某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )
某超市对某月(30天)每天顾客使用信用卡购物的人数进行了统计,得到如图所示的样本茎叶图,则该样本的中位数、众数、极差分别是( )| A. | 44,45,56 | B. | 44,43,56 | C. | 44,43,57 | D. | 45,43,57 |
13.已知复数z=$\frac{2i}{1+i}$,则z•$\overline z$=( )
| A. | 2 | B. | 2i | C. | 4 | D. | 4i |
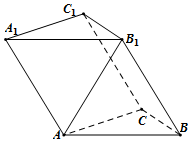 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.