题目内容
11.在(2x+1)(x-1)5的展开式中含x4项的系数是15.(用数字作答)分析 把多项式按乘法展开,将问题转化为二项展开式的系数问题;
利用二项展开式的通项公式求出展开式的通项,
分别令x的指数为3,4求出展开式含x3,x4项的系数;
再求(2x+1)(x-1)5展开式中含x4项的系数.
解答 解:(2x+1)(x-1)5=2x(x-1)5+(x-1)5,
∴(x+2)(x-1)5展开式中含x4项的系数为
(x-1)5展开式中x4系数与x3系数的2倍之和;
∵(x-1)5展开式的通项为Tr+1=(-1)rC5rx5-r,
令5-r=4,得r=1;
∴展开式中含x4的系数为-5;
令5-r=3,得r=2;
∴展开式中含x3的系数为10;
∴(2x+1)(x-1)5展开式中含x4项的系数为
(-5)+2×10=15.
故答案为:15.
点评 本题考查了等价转化的数学思想方法、以及利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
相关题目
19.$\frac{(x+y+1)^{5}}{xy}$展开式中的常数项为( )
| A. | 20 | B. | 10 | C. | 5 | D. | 1 |
6.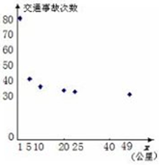 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
把界桩公里数1001记为x=1,公里数1005记为x=5,…,数据绘成的散点图如图所示,以x为解释变量、交通事故数y为预报变量,建立了两个不同的回归方程y(1)=29.9+50.2×$\frac{1}{x}$和y(2)=33.9+125.9e-x表述x,y二者之间的关系.
(Ⅰ)计算R2的值,判断这两个回归方程中哪个拟合效果更好?并解释更好的这个拟合所对R2的意义;
(Ⅱ)若保险公司在每次交通事故中理赔60万元的概率为0.01,理赔2万元的概率为0.19,理赔0.2万元的概率为0.8,利用你得到的拟合效果更好的这一个回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:对回归直线y=$\widehat{α}$+$\widehat{β}$x,有R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$.
一些量的计算值:
表中:${\widehat{{y}_{i}}}^{(1)}$=29.9+50.2×$\frac{1}{{x}_{i}}$,${\widehat{{y}_{i}}}^{(2)}$=33.9+125.9e${\;}^{-{x}_{i}}$,$\frac{1}{40}$=0.025,e-40≈0.
 经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:
经统计,2015年,某公路在部分界桩附近发生的交通事故次数如下表:| 界桩公里数 1001 | 1005 | 1010 | 1020 | 1025 | 1049 |
| 交通事故数 80 | 40 | 35 | 33 | 32 | 30 |
(Ⅰ)计算R2的值,判断这两个回归方程中哪个拟合效果更好?并解释更好的这个拟合所对R2的意义;
(Ⅱ)若保险公司在每次交通事故中理赔60万元的概率为0.01,理赔2万元的概率为0.19,理赔0.2万元的概率为0.8,利用你得到的拟合效果更好的这一个回归方程,试预报这一年在界桩1040公里附近处发生的交通事故的理赔费(理赔费精确到0.1万元).
附:对回归直线y=$\widehat{α}$+$\widehat{β}$x,有R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$.
一些量的计算值:
| $\overline{y}$ $\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(1)})^{2}$ | $\sum_{i=1}^{6}({y}_{i}-{\widehat{{y}_{i}}}^{(2)})^{2}$ |
| 41.7 1821 | 0.875 | 48.4 |
16.已知复数z=cosθ+isinθ(i为虚数单位),则$z•\overline{z}$=( )
| A. | cos2θ | B. | 1 | C. | cos2θ | D. | cos2θ+isinθ |
20.在1000个有机会中奖的号码(编号为000~999)中,按照随机抽取的方法确定后两位数为88的号码为中奖号码,该抽样运用的抽样方法是( )
| A. | 简单随机抽样 | B. | 系统抽样 | C. | 分层抽样 | D. | 抽签法 |
1.某产品的广告费用x(万元)与销售额y(万元)的统计数据如表:
根据表可得回归直线方程$\widehat{y}$=7x+$\widehat{a}$,若广告费用为10万元,则预计销售额为( )
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 73万元 | B. | 73.5万元 | C. | 74万元 | D. | 74.5万元 |
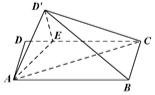 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.