题目内容
1.若函数$f(x)=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$在区间[-k,k](k>0)上的值域为[m,n],则m+n等于( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 由已知函数解析式可得f(x)+f(-x)=6,结合f(x)在区间[-k,k](k>0)上的值域为[m,n],即无论k取什么样的正实数都应有最大值与最小值的和是一个确定的值,令k=1得答案.
解答 解:∵$f(x)=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$,
∴f(-x)=3+$\frac{{2}^{-x}-1}{{2}^{-x}+1}+sin(-2x)$=3-$\frac{{2}^{x}-1}{{2}^{x}+1}-sin2x$,
∴f(x)+f(-x)=6.①
又f(x)在区间[-k,k](k>0)上的值域为[m,n],
即无论k取什么样的正实数都应有最大值与最小值的和是一个确定的值,
故可令k=1,由于函数$f(x)=3+\frac{{{2^x}-1}}{{{2^x}+1}}+sin2x$在区间[-k,k](k>0)上是一个增函数,
故m+n=f(k)+f(-k)
由①知,m+n=f(k)+f(-k)=6.
故选:D.
点评 本题考查函数的值域,考查函数的奇偶性与单调性的性质,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在等比数列{an}中,a1=1,a3=2a2,数列{an}前n项和Sn为( )
| A. | Sn=2n-1 | B. | Sn=2n-1 | C. | Sn=n2 | D. | Sn=2n-1 |
6.已知函数f(x)=$\sqrt{3}$sin(2x-φ)-cos(2x-φ)(|φ|<$\frac{π}{2}$)的图象关于y轴对称,则f(x)在区间$[{-\frac{π}{6},\frac{π}{3}}]$上的最大值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
13.已知函数$f(x)=\left\{\begin{array}{l}2{e^x},x<0\\{log_2}({x+1})+2,x≥0\end{array}\right.(e$为自然对数的底数),则不等式f(x)>4的解集为( )
| A. | (-ln2,0)∪(3,+∞) | B. | (-ln2,+∞) | C. | (3,+∞) | D. | (-ln2,0) |
10.现行普通高中学生在高一升高二时面临着选文理科的问题,学校抽取了部分男、女学生意愿的一份样本,制作出如下两个等高堆积条形图:
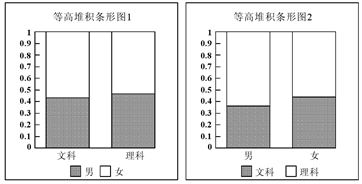
根据这两幅图中的信息,下列哪个统计结论是不正确的( )

根据这两幅图中的信息,下列哪个统计结论是不正确的( )
| A. | 样本中的女生数量多于男生数量 | |
| B. | 样本中有理科意愿的学生数量多于有文科意愿的学生数量 | |
| C. | 样本中的男生偏爱理科 | |
| D. | 样本中的女生偏爱文科 |
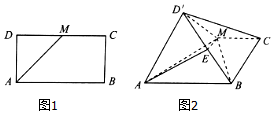 如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,AB=2$\sqrt{2}$,AD=$\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.