题目内容
设正△ABC的面积为2,边AB,AC的中点分别为D,E,M为线段DE上的动点,则
•
+
2的最小值为 .
| MB |
| MC |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,设正三角形ABC的边长为a,则
a2=2,解得a2=
.则B(-
a,0),C(
a,0),D(-
a,
a),E(
a,
a).设
=k
(0≤k≤1).可得
=
+k
=(
ka-
a,
a).
=(-
ka-
a,-
a),
=(
a-
ka,-
a),
2=a2.可得
•
+
2=
a2(k-
)2+
a2,再利用二次函数的单调性即可得出.
| ||
| 4 |
| 8 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| DM |
| DE |
| OM |
| OD |
| DE |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| MB |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| MC |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| BC |
| MB |
| MC |
| BC |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
解答:
解:如图所示,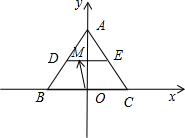
设正三角形ABC的边长为a,则
a2=2,解得a2=
.
则B(-
a,0),C(
a,0),D(-
a,
a),E(
a,
a).
设
=k
(0≤k≤1).
∴
=
+k
=(-
a,
a)+k(
a,0)=(
ka-
a,
a).
∴
=(-
ka-
a,-
a),
=(
a-
ka,-
a),
∴
•
+
2=(-
ka-
a)(
a-
ka)+
a2+a2
=a2(
k2-
k-
)+a2
=
a2(k-
)2+
a2,
当k=
时,
•
+
2的最小值为
a2=
×
=2
.
故答案为:2
.

设正三角形ABC的边长为a,则
| ||
| 4 |
| 8 | ||
|
则B(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
设
| DM |
| DE |
∴
| OM |
| OD |
| DE |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴
| MB |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| MC |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴
| MB |
| MC |
| BC |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
=a2(
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
当k=
| 1 |
| 2 |
| MB |
| MC |
| BC |
| 3 |
| 4 |
| 3 |
| 4 |
| 8 | ||
|
| 3 |
故答案为:2
| 3 |
点评:本题考查了向量的线性运算、数量积运算、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
函数y=
的图象大致是( )
| 1 |
| x-sinx |
A、 |
B、 |
C、 |
D、 |
已知f(x)=log2x+x-2,则零点所在的区间是( )
A、(0,
| ||
B、(
| ||
C、(1,
| ||
D、(
|
若双曲线
-
=1(a>0)的离心率为2,则a等于( )
| y2 |
| a2 |
| x2 |
| 3 |
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
 如图,四边形ABCD为矩形,AD⊥平面ABE,∠AEB=90°,F为CE上的点.
如图,四边形ABCD为矩形,AD⊥平面ABE,∠AEB=90°,F为CE上的点.