题目内容
已知偶函数f(x)满足f(x+1)=-
,且当x∈[-1,0]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-loga(x+2)有4个零点,则实数a的取值范围是 .
| 1 |
| f(x) |
考点:抽象函数及其应用,函数的零点与方程根的关系
专题:综合题,函数的性质及应用
分析:根据f(x+1)=-
,可得f(x)是周期为2的周期函数. 再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,可得函数在[-1,3]上的解析式.根据题意可得函数y=f(x)的图象与y=loga(x+2有4个交点,即可得实数a的取值范围.
| 1 |
| f(x) |
解答:
解:函数f(x)满足f(x+1)=-
,故有f(x+2)=f(x),
故f(x)是周期为2的周期函数.
再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,
可得当x∈[-1,0]时,f(x)=x2,故当x∈[-1,1]时,f(x)=x2 ,当x∈[1,3]时,f(x)=(x-2)2.
由于函数g(x)=f(x)-loga(x+2)有4个零点,故函数y=f(x)的图象与y=loga(x+2)有4个交点,
所以可得1≥loga(3+2),
∴实数a的取值范围是[5,+∞).
故答案为:[5,+∞).
| 1 |
| f(x) |
故f(x)是周期为2的周期函数.
再由f(x)是偶函数,当x∈[0,1]时,f(x)=x2,
可得当x∈[-1,0]时,f(x)=x2,故当x∈[-1,1]时,f(x)=x2 ,当x∈[1,3]时,f(x)=(x-2)2.
由于函数g(x)=f(x)-loga(x+2)有4个零点,故函数y=f(x)的图象与y=loga(x+2)有4个交点,
所以可得1≥loga(3+2),
∴实数a的取值范围是[5,+∞).
故答案为:[5,+∞).
点评:本题主要考查函数的周期性的应用,函数的零点与方程的根的关系,体现了转化的数学思想,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
复数z=
+ai(a∈R且a≠0)对应的点在复平面内位于( )
| 1 |
| a |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
函数f(x)的图象如图所示,则f(x)的解析式可能是( )


| A、f(x)=2lnx+x-1 | ||
| B、f(x)=2lnx-x+1 | ||
| C、f(x)=2xlnx | ||
D、f(x)=
|
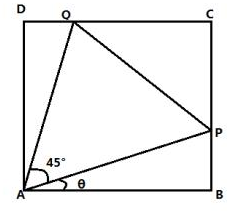 如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.
如图的正方形ABCD边长为1,P,Q为线段BC,CD上的动点,设∠PAB=θ,且tanθ=t,∠PAQ=45°.