题目内容
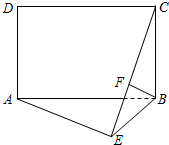
如图，四边形ABCD为矩形，AD⊥平面ABE，∠AEB=90°，F为CE上的点．（Ⅰ）求证：AD∥平面BCE；
（Ⅱ）求证：AE⊥BF．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（Ⅰ）直接根据已知条件，将利用线线平行转化为线面平行．
（Ⅱ）利用线面垂直转化成线线垂直，进一步利用线面垂直的判定得到线面垂直，最后证得线线垂直．
（Ⅱ）利用线面垂直转化成线线垂直，进一步利用线面垂直的判定得到线面垂直，最后证得线线垂直．
解答：
（本小题满分13分）
（Ⅰ）证明：因为四边形ABCD为矩形，
所以AD∥BC
又因为BC?平面BCE
AD?平面BCE
所以AD∥平面BCE
（Ⅱ）证明：因为AD⊥平面ABE
AD∥BC
BC⊥平面ABE
AE⊥BC
因为∠AEB=90°
所以：AE⊥BE
所以：AE⊥平面BCE
BF?平面BCE
所以：AE⊥BF
（本小题满分13分）（Ⅰ）证明：因为四边形ABCD为矩形，
所以AD∥BC
又因为BC?平面BCE
AD?平面BCE
所以AD∥平面BCE
（Ⅱ）证明：因为AD⊥平面ABE
AD∥BC
BC⊥平面ABE
AE⊥BC
因为∠AEB=90°
所以：AE⊥BE
所以：AE⊥平面BCE
BF?平面BCE
所以：AE⊥BF
点评：本题考查的知识要点：线面平行的判定，线面垂直的判定，及线面垂直与线线垂直之间的转化．属于基础题型．
练习册系列答案
启东小题作业本系列答案
相关题目
设全集U={0，1，2，3，4}，集合A={0，1，2}，集合b={2，3}，则（∁UA）∪B=（ ）
| A、∅ |
| B、{1，2，3，4} |
| C、{2，3，4} |
| D、{0，11，2，3，4} |
复数z=
+ai（a∈R且a≠0）对应的点在复平面内位于（ ）
| 1 |
| a |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
设集合A={4，5，6，8}，B={3，5，7，8}，则A∪B中元素的个数为（ ）
| A、8 | B、7 | C、6 | D、5 |