题目内容
已知函数f(x)=x2+2x的图象在点A(x1,f(x1))与点B(x2,f(x2))(x1<x2<0)处的切线互相垂直,则x2-x1的最小值为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:利用导数的几何意义即可得到切线的斜率,因为切线互相垂直,可得f′(x1)f′(x2)=-1,即(2x1+2)(2x2+2)=-1.可得x2-x1=
[-(2x1+2)+(2x2+2)],再利用基本不等式的性质即可得出.
| 1 |
| 2 |
解答:
解:∵x1<x2<0,∴f(x)=x2+2x+,∴f′(x)=2x+2,
∴函数f(x)在点A,B处的切线的斜率分别为f′(x1),f′(x2),
∵函数f(x)的图象在点A,B处的切线互相垂直,
∴f′(x1)f′(x2)=-1,
∴(2x1+2)(2x2+2)=-1.
∴2x1+2<0,2x2+2>0,
∴x2-x1=
[-(2x1+2)+(2x2+2)]≥
=1,当且仅当-(2x1+2)=2x2+2=1,
即x1=-
,x2=-
时等号成立.
∴函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2-x1的最小值为1.
故选:B.
∴函数f(x)在点A,B处的切线的斜率分别为f′(x1),f′(x2),
∵函数f(x)的图象在点A,B处的切线互相垂直,
∴f′(x1)f′(x2)=-1,
∴(2x1+2)(2x2+2)=-1.
∴2x1+2<0,2x2+2>0,
∴x2-x1=
| 1 |
| 2 |
| (2x1+2)(2x2+2) |
即x1=-
| 3 |
| 2 |
| 1 |
| 2 |
∴函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2-x1的最小值为1.
故选:B.
点评:本题主要考查了基本函数的性质、利用导数研究函数的单调性、导数的几何意义、基本不等式的性质,属于中档题.

练习册系列答案
相关题目
(x2-x+1)10展开式中x3项的系数为( )
| A、-210 | B、210 |
| C、30 | D、-30 |
若变量x,y满足约束条件
,则z=2x-y的最小值为( )
|
| A、4 | B、1 | C、0 | D、-1 |
已知α是平面,m,n是直线,且m⊥α,则下列命题不正确的是( )
| A、若m∥n,则n⊥a |
| B、若n⊥α,则m∥n |
| C、若n∥α,则m⊥n |
| D、若m⊥n,则n∥α |
已知a,b,c分别为△ABC内角A,B,C的对边,且a,b,c成等比数列,且B=
,则
+
=( )
| π |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
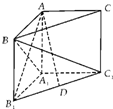 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=AC=AA1. (文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是
(文科)如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M、N分别是AD、BE的中点,将△ADE沿AE折起(D不在平面ABC内).下列说法正确的是