题目内容
18.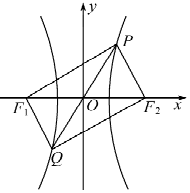 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
分析 由题意,矩形的对角线长相等,由此建立方程,找出a,c的关系,即可求出双曲线的离心率.
解答 解:由题意,矩形的对角线长相等,
y=$\sqrt{3}$x代入$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0),
可得x=±$\sqrt{\frac{{a}^{2}{b}^{2}}{{b}^{2}-3{a}^{2}}}$,y=±$\sqrt{3}$•$\sqrt{\frac{{a}^{2}{b}^{2}}{{b}^{2}-3{a}^{2}}}$,
∴$\frac{4{a}^{2}{b}^{2}}{{b}^{2}-3{a}^{2}}$=c2,
∴4a2b2=(b2-3a2)c2,
∴4a2(c2-a2)=(c2-4a2)c2,
∴e4-8e2+4=0,
∵e>1,∴e2=4+2$\sqrt{3}$,
∴e=$\sqrt{3}$+1.
故选:C.
点评 本题考查双曲线的离心率,考查矩形的性质,确定a,c的关系是关键,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.设向量$\overrightarrow{a}$=(-$\frac{1}{2}$,1),$\overrightarrow{b}$=(2,1),则|$\overrightarrow{a}$-$\overrightarrow{b}$|2=( )
| A. | $\frac{25}{4}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
6.已知向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{7}$,$\overrightarrow a•(\overrightarrow b-\overrightarrow a)=-4$,则$\overrightarrow a$与$\overrightarrow b$夹角是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
10.执行如图所示的程序框图,输出的n值为( )


| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
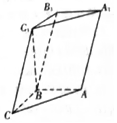 如图所示,三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.
如图所示,三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.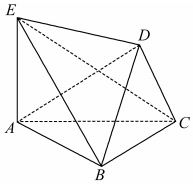 如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.
如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.