题目内容
10．执行如图所示的程序框图，输出的n值为（ ）
| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
分析 算法的功能是求S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n}}$的值，利用等比数列的前n项和公式求得满足条件S＞$\frac{1008}{2017}$的最小的n值．
解答 解：由程序框图知：算法的功能是求S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n}}$的值，
∵S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n}}$=$\frac{\frac{1}{3}（1-\frac{1}{{3}^{n}}）}{1-\frac{1}{3}}$＞$\frac{1008}{2017}$⇒n＞7，
∴跳出循环体的n值为8，∴输出n=8．
故选C．
点评 本题考查了循环结构的程序框图，根据框图的流程判断是否的功能是关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
18．
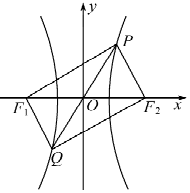已知F1，F2是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0$，b＞0）的左、右焦点，若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点，且四边形PF1QF2是矩形，则双曲线的离心率为（ ）
已知F1，F2是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0$，b＞0）的左、右焦点，若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点，且四边形PF1QF2是矩形，则双曲线的离心率为（ ）| A． | $5-2\sqrt{5}$ | B． | $5+2\sqrt{5}$ | C． | $\sqrt{3}+1$ | D． | $\sqrt{3}-1$ |
5．若复数$\frac{a+i}{1-i}$（i为虚数单位，a为实数）为纯虚数，则不等式|x+a|+|x|＞3的解集为（ ）
| A． | {x|x＞1} | B． | {x|x＜-2} | C． | {x|x＜-1或x＞2} | D． | {x|x＜-2或x＞1} |
2．若直线ax+y=0截圆x2+y2-2x-6y+6=0所得的弦长为$2\sqrt{3}$，则实数a=（ ）
| A． | 2 | B． | $\sqrt{3}$ | C． | $-\frac{3}{4}$ | D． | $-\frac{4}{3}$ |
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线为$y=\sqrt{5}x$，则双曲线的离心率为（ ）
| A． | $\frac{\sqrt{6}}{6}$ | B． | 2 | C． | $\sqrt{5}$ | D． | $\sqrt{6}$ |