题目内容
13.已知数列{an}与{bn}满足an+1-an=2(bn+1-bn),n∈N+,bn=2n-1,且a1=2.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设${c_n}=\frac{{{a_n}^n}}{{{b_n}^{n-1}}}$,Tn为数列{cn}的前n项和,求Tn.
分析 (I)计算an+1-an=4可得{an}是以2为首项,4为公差的等差数列,从而得出通项公式;
(II)计算得cn=(2n-1)•2n,使用错位相减法求出Tn.
解答 解:(Ⅰ)∵bn=2n-1,∴bn+1-bn=2n+1-2n+1=2,
∴an+1-an=2(bn+1-bn)=4,
∴{an}是以a1=2为首项,以4为公差的等差数列,
∴an=2+4(n-1)=4n-2.
(Ⅱ)${c_n}=\frac{{{a_n}^n}}{{{b_n}^{n-1}}}=\frac{{{{(4n-2)}^n}}}{{{{(2n-1)}^{n-1}}}}=(2n-1)•{2^n}$.
∴Tn=c1+c2+c3+…+cn=1•2+3•22+5•23+…+(2n-1)•2n,①
∴$2{T_n}=1•{2^2}+3•{2^3}+5•{2^4}+…+(2n-1)•{2^{n+1}}$,②
①-②得:$-{T_n}=1•2+2•{2^2}+2•{2^3}+…+2•{2^n}-(2n-1)•{2^{n+1}}$=$2+2[{\frac{{4(1-{2^{n-1}})}}{1-2}}]-(2n-1)•{2^{n+1}}$=-6-(2n-3)•2n+1,
∴${T_n}=6+(2n-3)•{2^{n+1}}$.
点评 本题考查了等差数列的判定,错位相减法求和,属于中档题.

练习册系列答案
相关题目
8.若不等式|x-2|+|x-3|<3的解集是(a,b),则$\int_a^b{(\sqrt{x}-1)dx=}$( )
| A. | $\frac{7}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{5}{3}$ | D. | 3 |
18.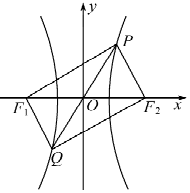 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
5.若复数$\frac{a+i}{1-i}$(i为虚数单位,a为实数)为纯虚数,则不等式|x+a|+|x|>3的解集为( )
| A. | {x|x>1} | B. | {x|x<-2} | C. | {x|x<-1或x>2} | D. | {x|x<-2或x>1} |
2.若直线ax+y=0截圆x2+y2-2x-6y+6=0所得的弦长为$2\sqrt{3}$,则实数a=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
3.${(x-\frac{1}{x})^6}$的展开式中含x2的项的系数是( )
| A. | -20 | B. | 20 | C. | -15 | D. | 15 |
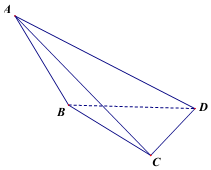 如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.
如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.