题目内容
6.已知向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{7}$,$\overrightarrow a•(\overrightarrow b-\overrightarrow a)=-4$,则$\overrightarrow a$与$\overrightarrow b$夹角是( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
分析 将$\overrightarrow a•(\overrightarrow b-\overrightarrow a)=-4$展开可得$\overrightarrow{a}•\overrightarrow{b}$,将|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$两边平方可求出|$\overrightarrow{b}$|,再代入向量的夹角公式计算即可.
解答 解:∵$\overrightarrow{a}(\overrightarrow{b}-\overrightarrow{a})$=$\overrightarrow{a}•\overrightarrow{b}-{\overrightarrow{a}}^{2}$=-4,${\overrightarrow{a}}^{2}$=|$\overrightarrow{a}$|2=1,
∴$\overrightarrow{a}•\overrightarrow{b}$=-3.
∵|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{7}$,即${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=7,
∴${\overrightarrow{b}}^{2}$=12,即|$\overrightarrow{b}$|=2$\sqrt{3}$.
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{\sqrt{3}}{2}$.
∵0≤<$\overrightarrow{a},\overrightarrow{b}$>≤π,
∴<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{5π}{6}$.
故选:A.
点评 本题考查了平面向量的数量积运算,属于基础题.

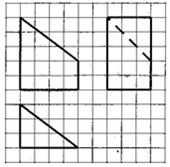
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
| A. | $[\frac{2}{3},11]$ | B. | [3,11] | C. | $[\frac{3}{2},11]$ | D. | [1,11] |
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
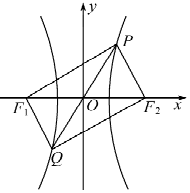 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
| A. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | B. | (x+$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | C. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | D. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{4}$ |