题目内容
7.已知向量$\overrightarrow{a}$=(1,3),向量$\overrightarrow{c}$满足|$\overrightarrow{c}$|=$\sqrt{10}$,若$\overrightarrow{a}$•$\overrightarrow{c}$=-5,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角大小为120°.分析 根据平面向量数量积的定义,写出数量积公式,即可求出$\overrightarrow{a}$与$\overrightarrow{c}$的夹角大小.
解答 解:向量$\overrightarrow{a}$=(1,3),向量$\overrightarrow{c}$满足|$\overrightarrow{c}$|=$\sqrt{10}$,
∴|$\overrightarrow{c}$|=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
∴$\overrightarrow{a}$•$\overrightarrow{c}$=-5,
∴|$\overrightarrow{a}$|×|$\overrightarrow{c}$|×cos<$\overrightarrow{a}$,$\overrightarrow{c}$>=$\sqrt{10}$×$\sqrt{10}$×cos<$\overrightarrow{a}$,$\overrightarrow{c}$>=-5,
∴cos<$\overrightarrow{a}$,$\overrightarrow{c}$>=-$\frac{1}{2}$,
∴$\overrightarrow{a}$与$\overrightarrow{c}$的夹角大小为120°.
故答案为:120°.
点评 本题考查了平面向量数量积的定义与应用问题,是基础题目.

练习册系列答案
相关题目
17.已知实数x,y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$,则$\frac{x+2y+3}{x+1}$的取值范围是( )
| A. | $[\frac{2}{3},11]$ | B. | [3,11] | C. | $[\frac{3}{2},11]$ | D. | [1,11] |
18.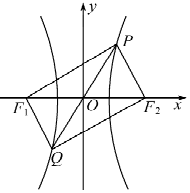 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
2.若直线ax+y=0截圆x2+y2-2x-6y+6=0所得的弦长为$2\sqrt{3}$,则实数a=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
16.一个圆经过椭圆$\frac{{x}^{2}}{4}$+y2=1的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为( )
| A. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | B. | (x+$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | C. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{16}$ | D. | (x-$\frac{3}{4}$)2+y2=$\frac{25}{4}$ |
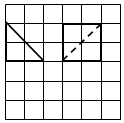 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为$\frac{8}{3}$,则该几何体的俯视图可以是( )