题目内容
9．设向量$\overrightarrow{a}$=（-$\frac{1}{2}$，1），$\overrightarrow{b}$=（2，1），则|$\overrightarrow{a}$-$\overrightarrow{b}$|2=（ ）| A． | $\frac{25}{4}$ | B． | $\frac{5}{2}$ | C． | 2 | D． | $\frac{1}{2}$ |
分析 利用向量坐标运算性质、模的计算公式即可得出．
解答 解：$\overrightarrow{a}-\overrightarrow{b}$=$（-\frac{5}{2}，0）$．
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|2=$\frac{25}{4}$．
故选：A．
点评 本题考查了向量坐标运算性质、模的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．已知实数x，y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$，则$\frac{x+2y+3}{x+1}$的取值范围是（ ）
| A． | $[\frac{2}{3}，11]$ | B． | [3，11] | C． | $[\frac{3}{2}，11]$ | D． | [1，11] |
14．函数f（x）=6cos（$\frac{3π}{2}$+x）-cos2x的最小值是（ ）
| A． | -7 | B． | -6 | C． | -5 | D． | -4 |
18．
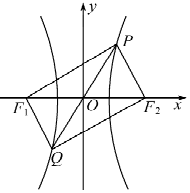已知F1，F2是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0$，b＞0）的左、右焦点，若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点，且四边形PF1QF2是矩形，则双曲线的离心率为（ ）
已知F1，F2是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0$，b＞0）的左、右焦点，若直线$y=\sqrt{3}x$与双曲线C交于P、Q两点，且四边形PF1QF2是矩形，则双曲线的离心率为（ ）| A． | $5-2\sqrt{5}$ | B． | $5+2\sqrt{5}$ | C． | $\sqrt{3}+1$ | D． | $\sqrt{3}-1$ |