题目内容
等差数列{an}中，d＜0，若|a3|=|a9|，的前n项和取最大值时，n的值为 ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：由题意可得等差数列{an}的前5项均为正值，第6项为0，从第7项开始为负值，进而可得答案．
解答：
解：∵等差数列{an}中d＜0，∴数列递减，
又∵|a3|=|a9|，∴a3＞0，且a9＜0，
∴a3=-a9，即a3+a9=0，
由等差数列的性质可得2a6=a3+a9=0，
∴等差数列{an}的前5项均为正值，第6项为0，从第7项开始为负值，
∴数列的前5项和等于前6项和最大．
故答案为：5或6
又∵|a3|=|a9|，∴a3＞0，且a9＜0，
∴a3=-a9，即a3+a9=0，
由等差数列的性质可得2a6=a3+a9=0，
∴等差数列{an}的前5项均为正值，第6项为0，从第7项开始为负值，
∴数列的前5项和等于前6项和最大．
故答案为：5或6
点评：本题考查等差数列的性质和前n项和的最值，得出数列项的变化是解决问题的关键，属中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
如果实数x、y满足条件
，那么z=-2x+y的最大值为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
定义在R上的函数f（x）满足f（4）=1，已知f（x）的导函数f（x）′的图象如图所示，若两个正数a、b满足f（2a+b）＜1，则| a+2b+3 |
| a+1 |
A、（
| ||||
B、（-∞，
| ||||
C、（
| ||||
| D、（-∞，3） |
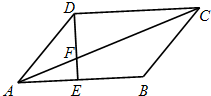如图，平行四边形ABCD中，AE：EB=1：2，若△AEF的面积等于1cm2 则△CDF的面积等于
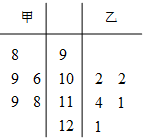在数学趣味知识培训活动中，甲、乙两名学生的5次培训成绩如图茎叶图所示：