题目内容
已知集合A={x|x2+2x-8=0}，B={x|x2-5x+6=0}，C={x|x2-mx+m2-19=0}，若B∩C≠∅，A∩C=∅，求m的值．
考点：交集及其运算
专题：集合
分析：求出A与B中方程的解确定出A与B，根据B∩C≠∅，A∩C=∅，求出m的值即可．
解答：
解：由A中方程变形得：（x-2）（x+4）=0，
解得：x=2或x=-4，即A={-4，2}；
由B中方程变形得：（x-2）（x-3）=0，
解得：x=2或x=3，即B={2，3}，
∵B∩C≠∅，A∩C=∅，
∴x=3为C中方程的解，
把x=3代入x2-mx+m2-19=0，得：9-3m+m2-19=0，即m2-3m-10=0，
解得：m=5（舍去）或m=-2，
则m=-2．
解得：x=2或x=-4，即A={-4，2}；
由B中方程变形得：（x-2）（x-3）=0，
解得：x=2或x=3，即B={2，3}，
∵B∩C≠∅，A∩C=∅，
∴x=3为C中方程的解，
把x=3代入x2-mx+m2-19=0，得：9-3m+m2-19=0，即m2-3m-10=0，
解得：m=5（舍去）或m=-2，
则m=-2．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
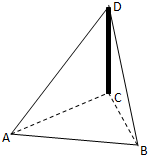如图所示，哈三中甲，乙两位同学分别站在新校区体育场内的A，B两点，利用三角函数知识测量锅炉房烟囱CD的高．已知AB=15米，∠DAC=60°，∠CAB=15°，∠CBA=45°，求烟囱CD的高．