题目内容
已知函数y=loga(-x2+log2ax)对任意x∈(0,
]都有意义,则实数a的范围是 .
| 1 |
| 2 |
考点:复合函数的单调性
专题:计算题,数形结合,函数的性质及应用
分析:由题意,-x2+log2ax>0在x∈(0,
]上恒成立,即log2ax>x2恒成立,可结合函数的图象求解.
| 1 |
| 2 |
解答:
 解:由题意,-x2+log2ax>0在x∈(0,
解:由题意,-x2+log2ax>0在x∈(0,
]上恒成立,即log2ax>x2恒成立,如图:
当2a>1时不符合要求;
当0<2a<1时,若y=log2ax过点(
,
),即
=log2a
,所以a=
,
故
<a<
,
综上所述,a的范围为:(
,
)
故答案为:(
,
)
 解:由题意,-x2+log2ax>0在x∈(0,
解:由题意,-x2+log2ax>0在x∈(0,| 1 |
| 2 |
当2a>1时不符合要求;
当0<2a<1时,若y=log2ax过点(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 32 |
故
| 1 |
| 32 |
| 1 |
| 2 |
综上所述,a的范围为:(
| 1 |
| 32 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 32 |
| 1 |
| 2 |
点评:本题考查对数函数的定义域、不等式恒成立问题,考查转化思想和数形结合思想.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
设l,m是两条不同的直线,a是一个平面,则下列命题正确的是( )
| A、若l⊥m,m⊥a,则l∥a |
| B、若m⊥l,l?a,则m⊥a |
| C、若m∥l,l∥a,则m∥a |
| D、若l⊥a,m⊥a,则l∥m |
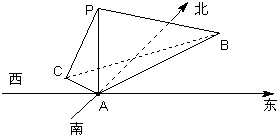 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
已知函数f(x)=x3+2x+sinx(x∈R),f(x1)+f(x2)>0,则下列不等式正确的是( )
| A、x1>x2 |
| B、x1<x2 |
| C、x1+x2<0 |
| D、x1+x2>0 |
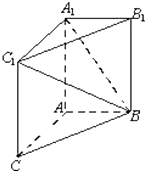 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.