题目内容
20.甲、乙两人玩儿掷骰子游戏,游戏规则规定:若抛掷处的点数不少于3点,则抛掷者得1分,对方得0分,若抛掷出的点数少于3点,则抛掷者得0分,对方得1分,各次抛掷互相独立,并规定第一次由甲抛掷,第二次由乙抛掷,第三次再由甲抛掷,依次轮换抛掷.(Ⅰ)求前3次抛掷甲得2分且乙得1分的概率;
(Ⅱ)ξ表示前3此抛掷乙的得分,求ξ的分布列及数学期望.
分析 (Ⅰ)设甲第一次抛掷大于等于3点为事件A,乙第一次抛掷大于等于3点为事件B,甲第二次抛掷大于等于3点为事件C,可得P(A)=P(B)=P(C)=$\frac{2}{3}$,P($\overline{A}$)=P($\overline{B}$)=P($\overline{C}$)=$\frac{1}{3}$.再由相互独立事件的概率求得前3次抛掷甲得2分且乙得1分的概率;
(Ⅱ)由题意求得ξ的取值,进一步求得对应的概率,得到分布列,代入期望公式求得数学期望.
解答 解:(Ⅰ)设甲第一次抛掷大于等于3点为事件A,乙第一次抛掷大于等于3点为事件B,甲第二次抛掷大于等于3点为事件C.
则P(A)=P(B)=P(C)=$\frac{2}{3}$,P($\overline{A}$)=P($\overline{B}$)=P($\overline{C}$)=$\frac{1}{3}$.
前3次抛掷甲得2分且乙得1分包括甲两次均大于等于3点乙大于等于3点;甲有1次不大于等于3点乙的1次不大于等于3点.
∴前3次抛掷甲得2分且乙得1分的概率P=$(P(A))^{2}P(B)+{C}_{2}^{1}P(A)P(\overline{A})P(\overline{B})$=$(\frac{2}{3})^{2}×\frac{2}{3}+2×\frac{2}{3}×\frac{1}{3}×\frac{1}{3}=\frac{4}{9}$;
(Ⅱ)ξ=0、1、2、3.
P(ξ=0)=$\frac{2}{3}×\frac{2}{3}×\frac{1}{3}=\frac{4}{27}$,P(ξ=1)=$\frac{4}{9}$,P(ξ=2)=$\frac{1}{3}$,P(ξ=3)=$\frac{1}{3}×\frac{2}{3}×\frac{1}{3}=\frac{2}{27}$.
分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{4}{27}$ | $\frac{4}{9}$ | $\frac{1}{3}$ | $\frac{2}{27}$ |
点评 本题考查离散型随机变量的期望与方差,考查了独立重复试验与相互独立事件的概率,是中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{4}{9}$ |
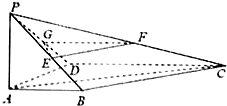 已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点.
已知如图,四边形ABCD是直角梯形,AB∥DC,AB⊥AD,AP⊥平面ABCD,DC=2AB=2AD=2AP,点E、F、G分别是PB、PC、PD的中点.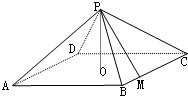 如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,
如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,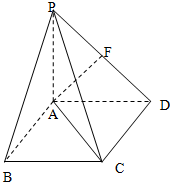 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.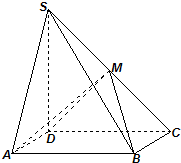 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.