题目内容
19．
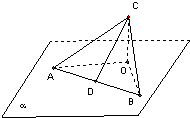如图：已知三角形ABC，∠ACB=90°，AB在平面α内，C不在平面α内，点C在平面α内的射影为O，CA，CB与平面α所成角分别为30°，45°，CD⊥AB，D为垂足，则CD与平面α所成角60°．
分析 设OC=a，利用勾股定理，求出AC，BC，AB，CD，可得sin∠CDO=$\frac{\sqrt{3}}{2}$，进而得到CD与平面α所成角．
解答 解：设OC=a，
∵CA，CB与平面α所成角分别为30°，45°，
∴AC=2a，BC=$\sqrt{2}$a，
AB=$\sqrt{6}$a，CD=$\frac{AC•BC}{AB}$=$\frac{2\sqrt{3}}{3}$a，
故sin∠CDO=$\frac{\sqrt{3}}{2}$，
故∠CDO=60°，
即CD与平面α所成角为60°，
故答案为：60°
点评 本题考查的知识点是直线与平面所成的角，难度中档．
练习册系列答案
相关题目
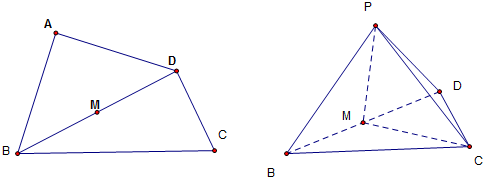
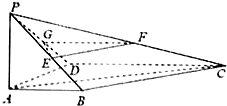已知如图，四边形ABCD是直角梯形，AB∥DC，AB⊥AD，AP⊥平面ABCD，DC=2AB=2AD=2AP，点E、F、G分别是PB、PC、PD的中点．
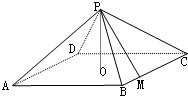如图：四棱锥P-ABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD=$\frac{π}{3}$，M是BC上的点，且BM=$\frac{1}{2}$，
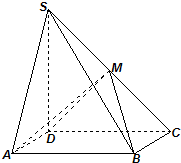如图，四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=$\sqrt{2}$，DC=SD=2，点M是侧棱SC的中点．