题目内容

6．在极坐标系中，点A在圆ρ2-2ρcosθ-4ρsinθ+4=0上，点P的坐标为（1，0），则|AP|的最小值为1．

分析 先将圆的极坐标方程化为标准方程，再运用数形结合的方法求出圆上的点到点P的距离的最小值．

解答 解：设圆ρ2-2ρcosθ-4ρsinθ+4=0为圆C，将圆C的极坐标方程化为：x2+y2-2x-4y+4=0，
再化为标准方程：（x-1）2+（y-2）2=1；

如图，当A在CP与⊙C的交点Q处时，|AP|最小为：
|AP|min=|CP|-rC=2-1=1，
故答案为：1．

点评 本题主要考查曲线的极坐标方程和圆外一点到圆上一点的距离的最值，难度不大．

练习册系列答案
相关题目
12．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（　　）
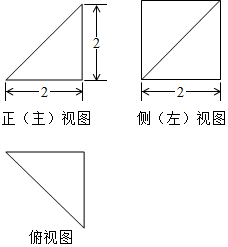
A．3$\sqrt{2}$B．2$\sqrt{3}$C．2$\sqrt{2}$D．2
17．若函数$f（x）=\sqrt{{2^x}-a}$的值域为[0，+∞），则a的取值范围是（0，+∞）．
14．已知数列{xn}满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，
（Ⅰ）0＜xn+1＜xn；
（Ⅱ）2xn+1-xn≤$\frac{{x}_{n}{x}_{n+1}}{2}$；
（Ⅲ）$\frac{1}{{2}^{n-1}}$≤xn≤$\frac{1}{{2}^{n-2}}$．
1．在平面直角坐标系xOy中，已知直线l的参数方程为$\left\{\begin{array}{l}{x=-8+t}\\{y=\frac{t}{2}}\end{array}\right.$（t为参数），曲线C的参数方程为$\left\{\begin{array}{l}{x=2{s}^{2}}\\{y=2\sqrt{2}}s\end{array}\right.$（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．
11．已知命题p：?x＞0，ln（x+1）＞0；命题q：若a＞b，则a2＞b2，下列命题为真命题的是（　　）
A．p∧qB．p∧￢qC．￢p∧qD．￢p∧￢q
18．已知当x∈[0，1]时，函数y=（mx-1）2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点，则正实数m的取值范围是（　　）
A．（0，1]∪[2$\sqrt{3}$，+∞）B．（0，1]∪[3，+∞）C．（0，$\sqrt{2}$）∪[2$\sqrt{3}$，+∞）D．（0，$\sqrt{2}$]∪[3，+∞）
15．设函数f（x）=2sin（ωx+φ），x∈R，其中ω＞0，|φ|＜π．若f（$\frac{5π}{8}$）=2，f（$\frac{11π}{8}$）=0，且f（x）的最小正周期大于2π，则（　　）
A．ω=$\frac{2}{3}$，φ=$\frac{π}{12}$B．ω=$\frac{2}{3}$，φ=-$\frac{11π}{12}$C．ω=$\frac{1}{3}$，φ=-$\frac{11π}{24}$D．ω=$\frac{1}{3}$，φ=$\frac{7π}{24}$
14．已知f（x）是定义在[-1，1]上的奇函数，且f（1）=1，若a，b∈[-1，1]，a+b≠0时，有$\frac{f（a）+f（b）}{a+b}$＞0成立．
（1）判断f（x）在[-1，1]上的单调性，并用定义证明；
（2）解不等式：f（2x-1）＞f（x2-1）；
（3）若f（x）≤m2-3am+1对所有的a∈[-1，1]恒成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网