题目内容
14.已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1],a+b≠0时,有$\frac{f(a)+f(b)}{a+b}$>0成立.(1)判断f(x)在[-1,1]上的单调性,并用定义证明;
(2)解不等式:f(2x-1)>f(x2-1);
(3)若f(x)≤m2-3am+1对所有的a∈[-1,1]恒成立,求实数m的取值范围.
分析 (1)设-1≤x1<x2≤1,令a=x1,b=-x2,利用奇函数的性质即可化简得出f(x1)<f(x2),得出结论;
(2)利用f(x)的单调性和定义域列不等式组解出;
(3)由题意可得m2-3am≥0恒成立,令g(a)=-3am+m2,讨论g(a)的单调性,令gmin(a)≥0即可得出m的范围.
解答 解:(1)f(x)在[-1,1]上为增函数,
证明:设x1,x2是[-1,1]上的任意两个数,且x1<x2,
令a=x1,b=-x2,则$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
∵x1-x2<0,
∴f(x1)-f(x2)<0,
∴f(x)在[-1,1]上是增函数.
(2)由题意得:$\left\{\begin{array}{l}{2x-1>{x}^{2}-1}\\{-1≤2x-1≤1}\\{-1≤{x}^{2}-1≤1}\end{array}\right.$,解得0<x≤1,
(3)∵f(x)是增函数,且f(1)=1,
∴1≤m2-3am+1恒成立,即m2-3am≥0恒成立,
令g(a)=-3am+m2,则gmin(a)≥0,
①若m=0,则g(a)=0,显然符合题意;
②若m>0,则gmin(a)=g(1)=-3m+m2≥0,解得m≥3,
③若m<0,则gmin(a)=g(-1)=3m+m2≥0,解得m≤-3,
综上,m的取值范围是(-∞,-3]∪[3,+∞)∪{0}.
点评 本题考查了函数的单调性判断与应用,函数恒成立问题与函数最值的计算,属于中档题.

练习册系列答案
相关题目
6.若回归直线的斜率$\widehatb∈(0,+∞)$,则相关系数r的取值范围为( )
| A. | (0,1] | B. | [-1,0) | C. | 0 | D. | 无法确定 |
3.已知f(x)=ln(e2x+1)+xcos2x,则f($\frac{π}{3}$)-f(-$\frac{π}{3}$)=( )
| A. | 0 | B. | $\frac{π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
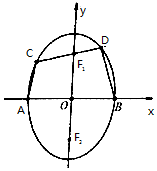 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.