题目内容
函数f(x)=sin(2x+φ)(|x|<π)的图象向左平移
个单位后关于原点对称,则函数f(x)在[0,
]上的最小值为( )
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数图象的平移得到y=sin[2(x+
)+ϕ]=sin(2x+
+ϕ),再由函数为奇函数及φ的范围得到
+ϕ=0
,求出φ的值,则函数解析式可求,再由x的范围求得函数f(x)在[0,
]上的最小值.
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
,求出φ的值,则函数解析式可求,再由x的范围求得函数f(x)在[0,
| π |
| 2 |
解答:
解:函数f(x)=sin(2x+φ)图象向左平移
个单位得y=sin[2(x+
)+ϕ]=sin(2x+
+ϕ),
由于函数图象关于原点对称,∴函数为奇函数,
又|φ|<
,∴
+ϕ=0,得ϕ=-
,
∴f(x)=sin(2x-
),
由于0≤x≤
,∴0≤2x≤π,
∴-
≤2x-
≤
,
当2x-
=-
,即x=0时,f(x)min=sin(-
)=-
.
故选:A.
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
由于函数图象关于原点对称,∴函数为奇函数,
又|φ|<
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
∴f(x)=sin(2x-
| π |
| 3 |
由于0≤x≤
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故选:A.
点评:本题考查了函数y=Asin(ωx+φ)型函数的图象和性质,考查了三角函数值域的求法,是中档题.

练习册系列答案
相关题目
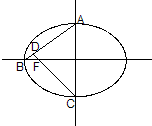 已知如图,椭圆的离心率为
已知如图,椭圆的离心率为| 1 |
| 2 |
A、-3
| ||
B、3-
| ||
C、3
| ||
D、3+
|
设甲、乙两名射手各打了5发子弹,每发子弹击中环数如下:
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
甲:10,6,7,10,8;
乙:8,7,9,10,9
则甲、乙两名射手的射击技术评定情况是( )
| A、甲比乙好 | B、乙比甲好 |
| C、甲、乙一样好 | D、难以确定 |