题目内容
已知函数f(x)=
,对于下列命题:
①函数f(x)的最小值为0;
②函数f(x)在R上是单调递减函数;
③若f(x)>1,则x<-1;
④若函数y=f(x)-a有三个零点,则a的取值范围是0<a<1.
其中正确命题的序号是 .
|
①函数f(x)的最小值为0;
②函数f(x)在R上是单调递减函数;
③若f(x)>1,则x<-1;
④若函数y=f(x)-a有三个零点,则a的取值范围是0<a<1.
其中正确命题的序号是
考点:分段函数的应用
专题:阅读型,数形结合,函数的性质及应用
分析:画出函数f(x)的图象,通过图象观察得到①函数f(x)无最大值和最小值,即可判断;②通过图象观察函数有增有减,即可判断②;③通过图象得到(
)x-1>1,由指数不等式的解法,得到x的解即可判断;④通过图象观察直线y=a与曲线有三个交点,即可得到a的取值范围.
| 1 |
| 2 |
解答:
解: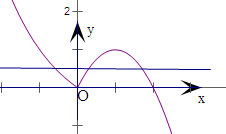 画出函数f(x)的图象,通过图象观察得到:
画出函数f(x)的图象,通过图象观察得到:
①函数f(x)无最大值和最小值,故①错;
②函数的增区间为(0,1),减区间为(-∞,0),(1,+∞)
故②错;
③若f(x)>1,则(
)x-1>1,得到x<-1.故③正确;
④若函数y=f(x)-a有三个零点,则作出y=a,如图得到
0<a<1.故④正确.
故答案为:③④.
 画出函数f(x)的图象,通过图象观察得到:
画出函数f(x)的图象,通过图象观察得到:①函数f(x)无最大值和最小值,故①错;
②函数的增区间为(0,1),减区间为(-∞,0),(1,+∞)
故②错;
③若f(x)>1,则(
| 1 |
| 2 |
④若函数y=f(x)-a有三个零点,则作出y=a,如图得到
0<a<1.故④正确.
故答案为:③④.
点评:本题考查分段函数的图象及应用,考查函数的单调性和应用,考查指数不等式的解法,同时考查数形结合的思想方法,属于基础题.

练习册系列答案
相关题目
若f(x)=|x|(x∈R),则下列函数说法正确的是( )
| A、f(x)为奇函数 |
| B、f(x)奇偶性无法确定 |
| C、f(x)为非奇非偶 |
| D、f(x)是偶函数 |
 某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表:
某市政府为了了解居民的生活用电情况,以使全市在用电高峰月份的居民生活不受影响,决定制定一个合理的月均用电标准.为了确定一个较为合理的标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,其样本统计结果如下图表: