题目内容

若θ为三角形中最大内角，则直线l：xtanθ+y+m=0的倾斜角的范围是（　　）
A、(0，
π
2
)∪(
π
2
，
2π
3
)
B、(
π
3
，
π
2
)∪(
π
2
，
2π
3
)
C、(0，
π
3
)∪(
π
3
，π)
D、(0，
π
2
)∪(
2π
3
，π)
考点：直线的一般式方程
专题：直线与圆
分析：首先根据关系式求出直线的斜率，进一步利用倾斜角和斜率的关系及三角形的最大角求出结果．
解答： 解：斜率k=-tanθ
由于θ为三角形中最大内角

所以：60°≤θ＜180°
①60≤θ＜90
所以tanθ≥√3
②90＜θ＜180
所以tanA＜0
若倾斜角p
所以tanp=-tanθ
所以tanp＞0或tanp≤-√3
所以0＜p＜
π
2
，
π
2
＜p＜
2π
3

故：倾斜角的范围：（0，
π
2
）∪(
π
2
，
2π
3
)
故选：A
点评：本题考查的知识要点：直线的倾斜角和斜率的关系
练习册系列答案
相关题目
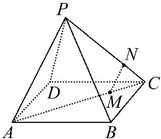如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（　　）
A、MN∥PD
B、MN∥PA
C、MN∥AD
D、以上均有可能
锐角△ABC的外接圆⊙O，且已知AB=4，∠C=45°，求外接圆的半径．
方程mx2+（2m+3）x+1-m=0有一个正根和一个负根的充要条件是
 
．
方程x3-2x2+3x-6=0在区间[-2，4]上的根必是属于区间
 
．
已知函数f（x）=x3-
3
4
x2sinθ，其中x∈R，θ为参数，且0≤θ≤π．若函数f（x）的极小值小于-
1
128
，则参数θ的取值范围是（　　）
A、（
π
6
，π）
B、（
π
6
，
π
2
]
C、[
π
6
，
5π
6
]
D、（
π
6
，
5π
6
）
如图，圆锥的侧面展开图恰好是一个半圆，则该圆锥的母线与底面所成的角的大小是
 
．
对于定义在R上的函数f（x），有下述四个命题，其中正确命题序号为
 
．
①若函数f（x）是奇函数，则f（x-1）的图象关于点A（1，0）对称；
②若对x∈R，有f（x+1）=f（x-1），则y=f（x）直线x=1对称；
③若函数f（x-1）关于直线x=1对称，则函数f（x）为偶函数；
④函数f（x+1）与函数f（1-x）直线x=1对称．
若方程
x2
a2
+
y2
b2
=1，a∈[1，5]，b∈[2，4]表示焦点在x轴上且离心率小于
3
2
的椭圆，则z=a+b的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网