题目内容
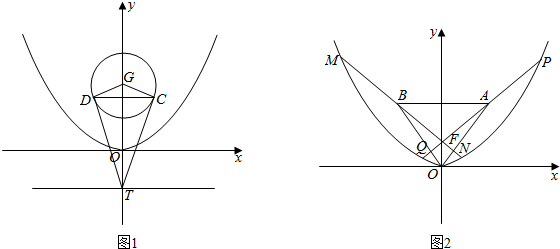
13.如图1.已知抛物线E的顶点O在坐标原点,焦点在y轴正半轴上,准线与y轴的交点为T.过点T作圆C:x2+(y-2)2=1的两条切线,两切点分别为D,G,且|DG|=$\frac{4\sqrt{2}}{3}$(1)求抛物线E的标准方程:
(2)如图2,过抛物线E的焦点F任作两条互相垂直线l1,l2,分别交抛物线E于P,Q两点和M,N两点,A,B分别为线段PQ和MN的中点.求△AOB面积的最小值.
分析 (1)设抛物线的方程为x2=2py(p>0),|CT|=2+$\frac{p}{2}$,再利用射影定理,即可求抛物线E的方程;
(2)设l1:y=kx+1,l2:y=-$\frac{1}{k}$x+1,P(x1,y1),Q(x2,y2),分别令直线PQ,MN与抛物线E联立方程组,求出A点和B点坐标,从而求出|AB|和O到AB的距离,求出△AOB面积,由此利用均值定理能求出△AOB面积的最小值.
解答 解:(1)设抛物线的方程为x2=2py(p>0),|CT|=2+$\frac{p}{2}$
设CT与DG交于E,则CE=$\sqrt{1-\frac{8}{9}}$=$\frac{1}{3}$,
∴1=$\frac{1}{3}$(2+$\frac{p}{2}$),
∴p=2,
∴抛物线E的标准方程为x2=4y;
(2)根据题意得l1,l2斜率存在
设l1:y=kx+1,l2:y=-$\frac{1}{k}$x+1
设P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$,可得x2-4kx-4=0,
∴x1+x2=4k,∴y1+y2=4k2+2,
∴A(2k,2k2+1)
同理可得B(-$\frac{2}{k}$,$\frac{2}{{k}^{2}}$+1)
∴直线AB的方程为y-(2k2+1)=(k-$\frac{1}{k}$)(x-2k),即(k-$\frac{1}{k}$)x-y+4=0,
∴O到AB的距离d=$\frac{4}{\sqrt{{k}^{2}+\frac{1}{{k}^{2}}-1}}$,
∵|AB|=2|k+$\frac{1}{k}$|$\sqrt{{k}^{2}+\frac{1}{{k}^{2}}-1}$,
∴△AOB面积S=$\frac{1}{2}$|AB|d=4|k+$\frac{1}{k}$|≥8,
当且仅当k=±1时,△AOB面积的最小值为8.
点评 本题考查抛物线方程的求法,考查三角形面积的最小值的求法,解题时要认真审题,注意均值定理的合理运用.

| A. | 2x+y-2=0 | B. | 2x-y-6=0 | C. | x-2y-6=0 | D. | x-2y+5=0 |
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |