题目内容
3.已知二次函数f(x)=ax2+ax-2b,其图象过点(2,-4),且f′(1)=-3.(Ⅰ)求a,b的值;
(Ⅱ)设函数h(x)=xlnx+f(x),求曲线h(x)在x=1处的切线方程.
分析 (Ⅰ)由题意可得f(2)=-4,代入f(x)解析式,求出f(x)的导数,代入x=1,解方程可得a=b=-1;
(Ⅱ)求出h(x)的解析式,求得导数,可得切线的斜率,再由点斜式方程可得切线的方程.
解答 解:(Ⅰ)由题意可得f(2)=-4,
即为4a+2a-2b=-4,
又f′(x)=2ax+a,可得f′(1)=3a=-3,
解方程可得a=b=-1;
(Ⅱ)函数h(x)=xlnx+f(x)
=xlnx-x2-x+2,
导数h′(x)=lnx+1-2x-1=lnx-2x,
即有曲线h(x)在x=1处的切线斜率为ln1-2=-2,
切点为(1,0),
则曲线h(x)在x=1处的切线方程为y-0=-2(x-1),
即为2x+y-2=0.
点评 本题主要考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用直线方程的点斜式方程是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
11.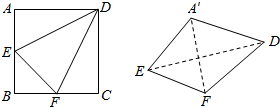 如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )
如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )
 如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )
如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )| A. | 8π | B. | 6π | C. | 11π | D. | 5π |
8.在△ABC中,内角A,B,C的对边分别是a,b,c,且满足bcosC=a,则△ABC的形状是( )
| A. | 等边三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
15.(x+1)2(x-2)4的展开式中含x3项的系数为( )
| A. | 16 | B. | 40 | C. | -40 | D. | 8 |
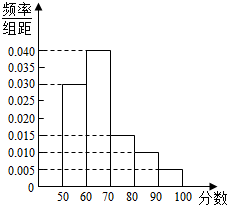 某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.
某次考试后,抽取了40位学生的成绩,并根据抽样数据制作的频率分布直方图如图所示,从成绩为[80,100]的学生中随机抽取了2人进行某项调查,则这两人分别来自两个不同分数段内的频率为$\frac{8}{15}$.