题目内容

1．已知抛物线x2=4y上的一点P到此抛物线的焦点的距离为2，则点P的纵坐标是（　　）
A．0B．$\frac{1}{2}$C．1D．2

分析 先根据抛物线方程求得焦点坐标及准线方程，进而根据抛物线的定义可知点p到焦点的距离与到准线的距离相等，进而推断出yp+1=2，求得yp．

解答 解：根据抛物线方程可求得焦点坐标为（0，1），准线方程为y=-1，
根据抛物线定义，
∴yp+1=2，
解得yp=1．
故选：C．

点评 本题主要考查抛物线的定义：抛物线上的点到焦点距离与到准线距离相等，常可用来解决涉及抛物线焦点的直线或焦点弦的问题．

练习册系列答案
相关题目
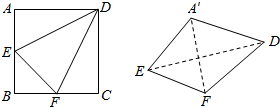11．如图，边长为2的正方形ABCD中，点E、F分别  是AB、BC的中点，将△ADE，△EBF，△FCD分别沿DE，EF，FD折起，使得A、B、C三点重合于点A′，若四面体A′EFD的四个顶点在同一个球面上，则该球的表面积为（　　）
A．8πB．6πC．11πD．5π
12．以下四个命题：
①若命题“?p”与“p或q”都是真命题，则命题q一定是真命题；
②若x≠kπ（k∈Z），则$sinx+\frac{1}{sinx}≥2$；
③?x0∈R，使$ln（{x_0^2+1}）＜0$；
④由曲线$y=x，y=\frac{1}{x}，\left|x\right|=2$围成的封闭图形的面积为$\frac{3}{2}-ln2$．
其中真命题的序号是①（把你认为真命题的序号都填上）．
9．给出下列命题：
（1）命题p：；菱形的对角线互相垂直平分，命题q：菱形的对角线相等；则p∨q是假命题
（2）命题“若x2-4x+3=0，则x=3”的逆否命题为真命题
（3）“1＜x＜3”是“x2-4x+3＜0”的必要不充分条件
（4）若命题p：?x∈R，x2+4x+5≠0，则?p：$?{x_0}∈R，{x_0}^2+4{x_0}+5=0$．
其中叙述正确的是（4）．（填上所有正确命题的序号）
16．已知抛物线C：y2=4x，焦点F，过点F任作直线l（不垂直于坐标轴）与曲线C交于A，B两点，由A，B分别向（x-1）2+y2=$\frac{1}{4}$各引一条切线，切点分别为P，Q，记α=∠AFP，β=∠BFQ，则cosα+cosβ=$\frac{1}{2}$．
6．已知函数f（x）=3x，对于定义域内任意的x1，x2（x1≠x2），给出如下结论：
①f（x1+x2）=f（x1）•f（x2）
②f（x1•x2）=f（x1）+f（x2）
③$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0
④f（-x1）+f（-x2）=f（x1）+f（x2）
其中正确结论的序号是（　　）
A．①③B．①④C．②③D．②④
13．如图1．已知抛物线E的顶点O在坐标原点，焦点在y轴正半轴上，准线与y轴的交点为T．过点T作圆C：x2+（y-2）2=1的两条切线，两切点分别为D，G，且|DG|=$\frac{4\sqrt{2}}{3}$
（1）求抛物线E的标准方程：
（2）如图2，过抛物线E的焦点F任作两条互相垂直线l1，l2，分别交抛物线E于P，Q两点和M，N两点，A，B分别为线段PQ和MN的中点．求△AOB面积的最小值．
10．已知函数f（x）=x2+alnx（a∈R，x∈[1，e]）．
（1）若a=-4时，求函数f（x）的最大值及相应的x的值；
（2）讨论方程f（x）=0的根的个数．
11．作一个以5cm为单位长度的圆，然后分别作出225°，330°角的正弦线，余弦线，正切线，量出它们的长度，从而写出这些角的正弦值、余弦值、正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网