题目内容
在△ABC中,角A,B,C对应的边分别是a,b,c.且满足(2a-c)cosB=bcosC,sin2A=sin2B+sin2C-λsinBsinC.(λ∈R).
(Ⅰ)求角B的大小;
(Ⅱ)若λ=
,求角C;
(Ⅲ)如果△ABC为钝角三角形,求λ的范围.
(Ⅰ)求角B的大小;
(Ⅱ)若λ=
| 3 |
(Ⅲ)如果△ABC为钝角三角形,求λ的范围.
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)已知第一个等式利用正弦定理化简,整理后根据sinA不为0求出cosB的值,即可确定出角B的大小;
(Ⅱ)已知第二个等式利用正弦定理化简得到关系式,利用余弦定理表示出cosA,把得出关系式及λ=
代入求出cosA的值,即可确定出角C;
(Ⅲ)表示出cosA,由三角形为钝角三角形,分A为钝角与C为钝角两种情况求出λ的范围即可.
(Ⅱ)已知第二个等式利用正弦定理化简得到关系式,利用余弦定理表示出cosA,把得出关系式及λ=
| 3 |
(Ⅲ)表示出cosA,由三角形为钝角三角形,分A为钝角与C为钝角两种情况求出λ的范围即可.
解答:
解:(Ⅰ)由(2a-c)cosB=bcosC得,(2sinA-sinC)cosB=sinBcosC,
整理得:2sinAcosB=sin(B+C)=sinA,
∵sinA≠0,∴cosB=
,
∵B∈(0,π),∴B=
;
(Ⅱ)由sin2A=sin2B+sin2C-λsinBsinC,(λ∈R),得:a2=b2+c2-λbc,
∴cosA=
=
=
,
∴A=
,
则C=
;
(Ⅲ)由(Ⅱ)知,cosA=
=
,
如果角A为钝角,即
<A<
,则有-
<
<0,
解得:-1<λ<0;
如果角C为钝角,0<A<
,则有
<
<1,
解得:
<λ<2,
综上,λ∈(-1,0)∪(
,2).
整理得:2sinAcosB=sin(B+C)=sinA,
∵sinA≠0,∴cosB=
| 1 |
| 2 |
∵B∈(0,π),∴B=
| π |
| 3 |
(Ⅱ)由sin2A=sin2B+sin2C-λsinBsinC,(λ∈R),得:a2=b2+c2-λbc,
∴cosA=
| b2+c2-a2 |
| 2bc |
| λ |
| 2 |
| ||
| 2 |
∴A=
| π |
| 6 |
则C=
| π |
| 2 |
(Ⅲ)由(Ⅱ)知,cosA=
| b2+c2-a2 |
| 2bc |
| λ |
| 2 |
如果角A为钝角,即
| π |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| λ |
| 2 |
解得:-1<λ<0;
如果角C为钝角,0<A<
| π |
| 6 |
| ||
| 2 |
| λ |
| 2 |
解得:
| 3 |
综上,λ∈(-1,0)∪(
| 3 |
点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图为函数y=sin(2x+φ)的图象,则φ的值可以为( )
如图为函数y=sin(2x+φ)的图象,则φ的值可以为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
P={(x,y)|x+y=5,x∈N*,y∈N*},则集合的非空子集的个数是( )
| A、3 | B、4 | C、15 | D、16 |
下列函数与函数y=x相等的是( )
| A、y=logaax(a>0,a≠1) | ||
B、y=
| ||
C、y=
| ||
D、y=(
|
如图,在正方体ABCD-A1B1C1D1中,AC与A1D所在直线所成的角等于( )
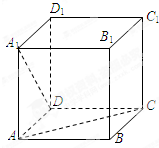

| A、30° | B、45° |
| C、60° | D、90° |
 2014年10月24日,成都七中第35届校运动会正在举行,如图所示,AB=90m,BC=30m,矩形DEFG为禁行区,EF=10m,DE=5m,联络员甲为尽快从D到B,先从D沿DG以每秒2m的速度到达线段DC上某处P,再从P处以每秒4m的速度直接到B,设DP=xm,则联络员甲从D到B的时间t(秒)与x(m)的函数关系式为
2014年10月24日,成都七中第35届校运动会正在举行,如图所示,AB=90m,BC=30m,矩形DEFG为禁行区,EF=10m,DE=5m,联络员甲为尽快从D到B,先从D沿DG以每秒2m的速度到达线段DC上某处P,再从P处以每秒4m的速度直接到B,设DP=xm,则联络员甲从D到B的时间t(秒)与x(m)的函数关系式为