题目内容
已知向量
=（2，m），
=（1，
），且向量
在向量
方向上的投影为1，则|
|= ．
| OA |
| OB |
| 3 |
| OA |
| OB |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的数量积公式得到向量的投影公式得到关于m的方程解之；再由有向线段
=
-
，得到所求．
| AB |
| OB |
| OA |
解答：
解：由已知向量
=（2，m），
=（1，
），且向量
在向量
方向上的投影为1，
所以向量|
|cos＜
，
＞=
=1=
，解得m=0，
所以
=
-
=（-1，
），所以|
|=2；
故答案为：2．
| OA |
| OB |
| 3 |
| OA |
| OB |
所以向量|
| OA |
| OA |
| OB |
| ||||
|
|
2+
| ||
| 2 |
所以
| AB |
| OB |
| OA |
| 3 |
| AB |
故答案为：2．
点评：本题考查了向量的坐标运算以及向量的投影、模的求法；属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
设集合A={{x|y=
}，集合B={x||x-2|＜2}，则A∩B等于（ ）
| 2+x-x2 |
| A、（0，2] | B、[0，2] |
| C、[-1，2） | D、∅ |
函数y=x2-4ax+1在区间[-2，4]上单调递增函数，则实数a的取值范围是（ ）
| A、（-∞，2] |
| B、（-∞，-1] |
| C、[2，+∞） |
| D、[-1，+∞） |
正三棱柱ABC-A1B1C1中，点D是BC的中点，BC=2，BB1=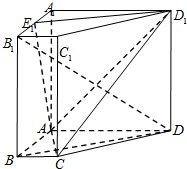
如图，在四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面 ABCD，底面ABCD是直角梯形，AD∥BC，∠BAD=90°，AD=AA1=3，BC=1，E1为A1B1中点．
如图，已知椭圆C：