题目内容
已知函数y=
,则y′= .
| sin(2x-1) |
| x-1 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则和复合函数的导数法则即可求出.
解答:
解:∵y=
,
∴y′=
,
故答案为:
| sin(2x-1) |
| x-1 |
∴y′=
| 2(x-1)cos(2x-1)-sin(2x-1) |
| (x-1)2 |
故答案为:
| 2(x-1)cos(2x-1)-sin(2x-1) |
| (x-1)2 |
点评:本题考查了导数的运算法则和复合函数的导数法则,属于基础题.

练习册系列答案
相关题目
若集合A={x|1gx<1},B={y|y=sinx,x∈R},则A∩B=( )
| A、(0,1) | B、(0,1] |
| C、[-1,1] | D、∅ |
某四棱柱的三视图如图所示,该几何体的各面中互相垂直的面的对数是( )


| A、2 | B、4 | C、6 | D、8 |
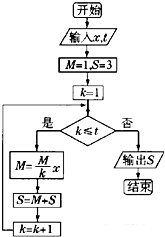 执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )
执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
|
| 1 |
| x |
A、e-
| ||
| B、1 | ||
| C、0 | ||
D、e
|
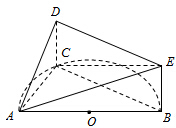 如图,半圆O的直径AB长为4,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,sin∠EAB=
如图,半圆O的直径AB长为4,C是半圆O上除A,B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,sin∠EAB=