题目内容
7.某几何体的三视图如图所示,若该几何体的体积为$\frac{20}{3}$,则图中x的值为( )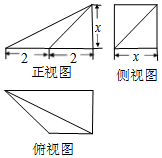
| A. | 3 | B. | 1 | C. | 2 | D. | $\frac{5}{2}$ |
分析 如图所示,该几何体为三棱柱ABC-A1B1C1,去掉一个三棱锥A-CDC1后剩下的几何体.其中AB⊥BC,侧面ABB1A1是正方形,D为BC的中点,BC=4.
解答 解:如图所示,该几何体为三棱柱ABC-A1B1C1,
去掉一个三棱锥A-CDC1后剩下的几何体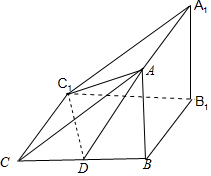 .
.
其中AB⊥BC,侧面ABB1A1是正方形,
D为BC的中点,BC=4.
∴该几何体的体积为$\frac{20}{3}$=$\frac{1}{2}•4x•x$-$\frac{1}{3}•\frac{1}{2}•2x$•x,
解得x=2.
故选:C.
点评 本题考查了三棱锥与三棱柱的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.若偶函数f(x)在(-∞,0]上单调递减,a=log2$\frac{1}{3}$,b=log4$\frac{1}{5}$,c=${2^{\frac{3}{2}}}$,则f(a),f(b),f(c)满足( )
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(a)<f(c) | C. | f(c)<f(a)<f(b) | D. | f(c)<f(b)<f(a) |
18.直线l1:ax+y-a+1=0,直线l1:4x+ay-2=0,则“a=±2”是“l1∥l2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
16.数列{an}满足a1=1,且对于任意的n∈N*都有an+1=an+a1+n,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2017}}}}$等于( )
| A. | $\frac{2016}{2017}$ | B. | $\frac{4032}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{4034}{2018}$ |
17.记不等式组$\left\{\begin{array}{l}4x+3y≥10\\ x≤3\\ y≤4\end{array}\right.$表示的平面区域为D,过区域D中任意一点P作圆x2+y2=1的两条切线,切点分别为A,B,则cos∠PAB的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |