题目内容
11.已知圆C1:x2+y2=9与圆C2:x2+y2-2x+2ky+k2-3=0.若圆C1与圆C2外切,则圆C1与圆C2的内公切线的方程为x$±2\sqrt{6}$y-15=0.分析 利用圆系方程求出直线方程,利用圆心到直线的距离与半径的关系求解即可.
解答 解:圆C1:x2+y2=9的圆心(0,0)半径为3,与圆C2:x2+y2-2x+2ky+k2-3=0.的圆心(1,k),半径为:2,
两个圆外切可得:$\sqrt{1+{k}^{2}}=5$,解得k=$±2\sqrt{6}$.
则圆C1与圆C2的内公切线的方程为:2x-2ky-k2-6=0,即:x$±2\sqrt{6}$y-15=0
故答案为:x$±2\sqrt{6}$y-15=0.
点评 本题考查两个圆的位置关系的应用,切线方程的求法,考查计算能力.

练习册系列答案
相关题目
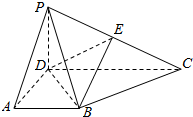 四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.
四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.