题目内容
3．二次函数y=ax2+2ax+1（a＜0）在区间[-1，4]上的最大值为4，则a的值为-3．分析 根据函数解析式确定函数对称轴，通过单调性确定最大值点，建立等量关系求解a的值．
解答 解：根据所给二次函数解析式可知，
对称轴为x=-1，
当a＜0时，函数在[-1，4]上单调递减，
所以函数在x=-1处取得最大值，
f（-1）=-a+1=4，所以a=-3．
故答案为：-3．
点评 本题考察二次函数的性质，对于给出最值求参问题，一般要结合题中所给解析式大致确定函数图象、运用单调性来研究．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14．已知tan$\frac{α}{2}$=3，则cosα-sinα=（ ）
| A． | $\frac{4}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{7}{5}$ | D． | -$\frac{7}{5}$ |
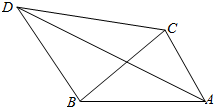如图，在△ABC中，AB=$\sqrt{2}$，AC=1，以BC为边作等腰直角三角形BCD（B为直角顶点，A，D两点在直线BC的两侧），当∠A∈[$\frac{π}{6}$，$\frac{2π}{3}$]时，$\overrightarrow{AC}$•$\overrightarrow{AD}$的取值范围是[$\frac{\sqrt{6}-\sqrt{2}}{2}$，2]．
12．函数f（x）=2x-2+ex-1的零点所在区间为（ ）
| A． | （-1，0） | B． | （0，1） | C． | （1，2） | D． | （2，3） |