题目内容
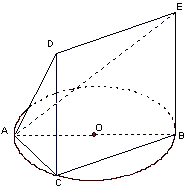 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,DC=| 3 |
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE?证明你的结论.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据图形可看出,三棱锥C-ABE的体积等于三棱锥E-ABC,容易得出BE⊥平面ABC,即BE是三棱锥E-ABC的高.并且容易知道底面△ABC是直角三角形,根据已知的边的长度即可求△ABC的面积,高BE=
,所以根据三棱锥的体积公式即可求出三棱锥E-ABC的体积,也就求出了三棱锥C-ABE的体积;
(2)根据已知条件容易证明BC⊥平面ACD,又DE∥BC,所以DE⊥平面ACD,DE?平面ADE,∴平面ACD⊥平面ADE;
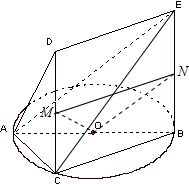
(3)要找M点使MO∥平面ADE,只要找OM所在平面,使这个平面和平面ADE平行,容易发现这个平面是:分别取DC,EB中点M,N,连接OM,MN.ON,则平面MON便是所找平面,容易证明该平面与平面ADE平行,所以MO∥平面ADE.
| 3 |
(2)根据已知条件容易证明BC⊥平面ACD,又DE∥BC,所以DE⊥平面ACD,DE?平面ADE,∴平面ACD⊥平面ADE;
(3)要找M点使MO∥平面ADE,只要找OM所在平面,使这个平面和平面ADE平行,容易发现这个平面是:分别取DC,EB中点M,N,连接OM,MN.ON,则平面MON便是所找平面,容易证明该平面与平面ADE平行,所以MO∥平面ADE.
解答:
 解:(1)如图,根据图形知道,三棱锥C-ABE的体积等于三棱锥E-ABC的体积;
解:(1)如图,根据图形知道,三棱锥C-ABE的体积等于三棱锥E-ABC的体积;
∵四边形DCBE为平行四边形,∴EB∥DC,又DC⊥平面ABC,∴EB⊥平面ABC;
AB是圆O的直径,∴∠ACB=90°,AC=
=
,BE=
;
∴V三棱锥C-ABE=V三棱锥E-ABC=
•
•
•1•
=
;
(2)DC⊥平面ABC,BC?平面ABC,∴DC⊥BC,⊥即BC⊥DC,又BC⊥AC,DC∩AC=C;
∴BC⊥平面ACD,DE∥BC;
∴DE⊥平面ACD,DE?平面ADE;
∴平面ADE⊥平面ACD,即平面ACD⊥平面ADE;
(3)在CD上存在一点M,是CD的中点,使得MO∥平面ADE,下面给出证明;
证明:取DC中点M,EB中点N,连接OM,MN,ON,∵O,M,N三点是中点,∴MN∥DE,ON∥AE;
∵AE,DE?平面ADE,ON,MN?平面ADE;
∴MN∥平面ADE,ON∥平面ADE,MN∩ON=N;
∴平面MON∥平面ADE,MO?平面MON;
∴MO∥平面ADE;
 解:(1)如图,根据图形知道,三棱锥C-ABE的体积等于三棱锥E-ABC的体积;
解:(1)如图,根据图形知道,三棱锥C-ABE的体积等于三棱锥E-ABC的体积;∵四边形DCBE为平行四边形,∴EB∥DC,又DC⊥平面ABC,∴EB⊥平面ABC;
AB是圆O的直径,∴∠ACB=90°,AC=
| 4-1 |
| 3 |
| 3 |
∴V三棱锥C-ABE=V三棱锥E-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
(2)DC⊥平面ABC,BC?平面ABC,∴DC⊥BC,⊥即BC⊥DC,又BC⊥AC,DC∩AC=C;
∴BC⊥平面ACD,DE∥BC;
∴DE⊥平面ACD,DE?平面ADE;
∴平面ADE⊥平面ACD,即平面ACD⊥平面ADE;
(3)在CD上存在一点M,是CD的中点,使得MO∥平面ADE,下面给出证明;
证明:取DC中点M,EB中点N,连接OM,MN,ON,∵O,M,N三点是中点,∴MN∥DE,ON∥AE;
∵AE,DE?平面ADE,ON,MN?平面ADE;
∴MN∥平面ADE,ON∥平面ADE,MN∩ON=N;
∴平面MON∥平面ADE,MO?平面MON;
∴MO∥平面ADE;
点评:考查三棱锥的体积公式,线面垂直的性质,线面垂直的判定定理,面面垂直的判定定理,中位线的性质,线面平行的判定定理,面面平行的判定定理,面面平行的性质.

练习册系列答案
相关题目
若直线l:x=a的倾斜角为α,则α=( )
| A、0 | ||
B、
| ||
C、
| ||
| D、不存在 |
已知P={x|y=
},Q={y|y=
},则下列结论正确的是( )
| x-1 |
| x-1 |
| A、P=Q | B、P∪Q=R |
| C、P?Q | D、Q?P |
已知奇函数f(x)在(-∞,0)上是单调减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A、{x|-3<x<-1} |
| B、{x|-1<x<1或1<x<3} |
| C、{x|-3<x<0或1<x<3} |
| D、{x|-3<x<1或x>2} |
 将各项均为正整数的数列{an}排成如图所示的三角形数阵(第n行有n个数;在同一行中,各项的下标从左到右依次增大).bn表示该数阵中第n行第1个数.已知数列{bn}为公比为q等比数列,a1=1,a3=a2+1,且从第3行开始,从左到右,各行均构成公差为d的等差数列.
将各项均为正整数的数列{an}排成如图所示的三角形数阵(第n行有n个数;在同一行中,各项的下标从左到右依次增大).bn表示该数阵中第n行第1个数.已知数列{bn}为公比为q等比数列,a1=1,a3=a2+1,且从第3行开始,从左到右,各行均构成公差为d的等差数列.