题目内容
国家统计局对某门户网站的访问量与广告收益进行统计评估,从该网站近三年中随机抽取100天,访问量的统计结果(单位:万次)如表所示:
(Ⅰ)根据上表的统计结果,求访问量分别为500万次,600万次,700万次的频率;
(Ⅱ)已知每100万次的访问量能使该网站获得广告收益5万元,用ξ表示该网站两天的广告收益(单位:
万元),假设每天的访问量相互独立,求ξ的分布列和数学期望.
| 访问量 | 500 | 600 | 700 |
| 频 数 | 50 | 30 | 20 |
(Ⅱ)已知每100万次的访问量能使该网站获得广告收益5万元,用ξ表示该网站两天的广告收益(单位:
万元),假设每天的访问量相互独立,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)依题设,能求出访问量分别为500万次,600万次,700万次的频率.
(Ⅱ)由题设知访问量分别为500万次,600万次,700万次的广告收益是25万元,30万元,35万元,相应的ξ的允许值为50,55,60,65,70,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(Ⅱ)由题设知访问量分别为500万次,600万次,700万次的广告收益是25万元,30万元,35万元,相应的ξ的允许值为50,55,60,65,70,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答:
解:(Ⅰ)依题设,访问量分别为500万次,600万次,700万次的频率分别为:
=0.5,
=0.3,
=0.2. …4分
(Ⅱ)由题设知访问量分别为500万次,600万次,700万次的广告收益是25万元,30万元,35万元,
相应的ξ的允许值为50,55,60,65,70.…5分
并且由题设中“每天的访问量相互独立”知:
P(ξ=50)=0.52=0.25,
P(ξ=55)=2×0.5×0.3=0.3,
P(ξ=60)=0.32+2×0.2×0.5=0.29,
P(ξ=65)=2×0.2×0.3=0.12,
P(ξ=70)=0.22=0.04.
于是,所求随机变量ξ的分布列为:
…11分
其期望Eξ=50×0.25+55×0.3+60×0.29+65×0.12+70×0.04=57(万元). …12分.
| 50 |
| 100 |
| 30 |
| 100 |
| 20 |
| 100 |
(Ⅱ)由题设知访问量分别为500万次,600万次,700万次的广告收益是25万元,30万元,35万元,
相应的ξ的允许值为50,55,60,65,70.…5分
并且由题设中“每天的访问量相互独立”知:
P(ξ=50)=0.52=0.25,
P(ξ=55)=2×0.5×0.3=0.3,
P(ξ=60)=0.32+2×0.2×0.5=0.29,
P(ξ=65)=2×0.2×0.3=0.12,
P(ξ=70)=0.22=0.04.
于是,所求随机变量ξ的分布列为:
| ξ | 50 | 55 | 60 | 65 | 70 |
| P | 0.25 | 0.3 | 0.29 | 0.12 | 0.04 |
其期望Eξ=50×0.25+55×0.3+60×0.29+65×0.12+70×0.04=57(万元). …12分.
点评:本题考查频率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知奇函数f(x)在(-∞,0)上是单调减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A、{x|-3<x<-1} |
| B、{x|-1<x<1或1<x<3} |
| C、{x|-3<x<0或1<x<3} |
| D、{x|-3<x<1或x>2} |
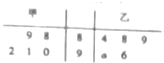 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数