题目内容
2.求值域:f(x)=4-$\frac{1}{\sqrt{{2}^{x}-1}}$.分析 利用指数函数的单调性、反比例函数的单调性即可得出.
解答 解:由2x-1>0,解得x>0,可得函数f(x)的定义域为{x|x>0}.
由2x-1>0,可得$\frac{1}{\sqrt{{2}^{x}-1}}$>0,
∴4-$\frac{1}{\sqrt{{2}^{x}-1}}$<4.
∴函数f(x)=4-$\frac{1}{\sqrt{{2}^{x}-1}}$的值域为(-∞,4).
点评 本题考查了指数函数的单调性、反比例函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.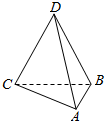 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
 已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )
已知如图所示的三棱锥D-ABC的四个顶点均在球O的球面上,△ABC和△DBC所在平面相互垂直,AB=3,AC=$\sqrt{3}$,BC=CD=BD=2$\sqrt{3}$,则球O的表面积为( )| A. | 4π | B. | 12π | C. | 16π | D. | 36π |
14.已知函数f(x)=x2+2x+a-1,当x∈(-∞,-3)时,f(x)>0恒成立.则实数a的取值范围是( )
| A. | a>-2 | B. | a≥-2 | C. | a>2 | D. | a≥2 |