题目内容
15．函数f（x）=a2x-4+2（a＞0且a≠1）的图象恒过定点是（2，3）．分析 根据指数函数恒过定点（0，1），即可求出结论．
解答 解：∵函数f（x）=a2x-4+2（a＞0且a≠1），
令2x-4=0，解得x=2；
∴y=f（2）=20+2=3，
∴函数f（x）的图象恒过定点（2，3）．
故答案为：（2，3）．
点评 本题考查了指数函数恒过定点的应用问题，是基础题目．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
6．若z（1+i）=2+i（i是虚数单位），则z=（ ）
| A． | $\frac{3}{2}+\frac{i}{2}$ | B． | $\frac{3}{2}-\frac{i}{2}$ | C． | $-\frac{3}{2}-\frac{i}{2}$ | D． | $-\frac{3}{2}+\frac{i}{2}$ |
7．已知$sinα=\frac{3}{5}$，则$sin（\frac{π}{2}+2α）$=（ ）
| A． | $-\frac{12}{25}$ | B． | $\frac{7}{25}$ | C． | $\frac{12}{25}$ | D． | $-\frac{7}{25}$ |
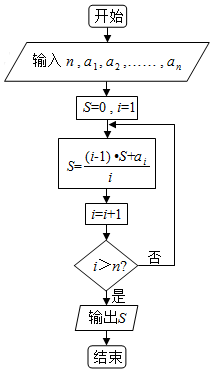执行如图所示的程序框图，若输入数据n=5，a1=-2，a2=-2.6，a3=3.2，a4=2.5，a5=1.4，则输出的结果为0.5．