题目内容
10.函数y=ax2+bx与$y={log_{|{\frac{b}{a}}|}}x(ab≠0,|a|≠|b|)$在同一直角坐标系中的图象可能是( )| A. | 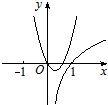 | B. |  | C. | 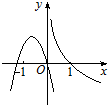 | D. | 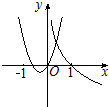 |
分析 方程ax2+bx=0的解为x=0或x=-$\frac{b}{a}$,图象分析|$\frac{b}{a}$|的取值范围,从而解得.
解答 解:方程ax2+bx=0的解为x=0或x=-$\frac{b}{a}$,
对于选项A,由二次函数知0<|$\frac{b}{a}$|<1,
由对数函数知|$\frac{b}{a}$|>1,故不可能;
对于选项B,由二次函数知0<|$\frac{b}{a}$|<1,
由对数函数知|$\frac{b}{a}$|>1,故不可能;
对于选项C,由二次函数知|$\frac{b}{a}$|>1,
由对数函数知0<|$\frac{b}{a}$|<1,故不可能;
对于选项D,由二次函数知0<|$\frac{b}{a}$|<1,
由对数函数知0<|$\frac{b}{a}$|<1,故有可能成立;
故选:D.
点评 本题考查了方程与函数的关系应用及数形结合的思想方法应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知直线l的斜率k满足-1≤k<1,则它的倾斜角α的取值范围是( )
| A. | $-\frac{π}{4}<α<\frac{π}{4}$ | B. | $-\frac{π}{4}≤α<\frac{π}{4}$ | C. | $0<α<\frac{π}{4}$或$\frac{3π}{4}<α<π$ | D. | $0≤α<\frac{π}{4}$或$\frac{3π}{4}≤α<π$ |
18.函数y=logax(a>0且a≠1)的反函数的图象经过点(2,4),则a的值为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
5.若定义在区间D上的函数f(x)对于D上任意n个值x1,x2,…xn总满足$\frac{1}{n}$[f(x1)+f(x2)+…+f(xn)]≤f($\frac{{x}_{1}{+x}_{2}+…{+x}_{n}}{n}$),则称f(x)为D的凸函数,现已知f(x)=sinx在(0,π)上是凸函数,则三角形ABC中,sinA+sinB+sinC的最大值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3 |