题目内容
8.已知数列{an},其通项公式an=nsin2$\frac{n}{2}$π-ncos2$\frac{n}{2}$π,其前n项和为Sn,求S2014+S2015的值.分析 an=nsin2$\frac{n}{2}$π-ncos2$\frac{n}{2}$π=-ncosnπ=(-1)n-1n,利用“分组求和”即可得出.
解答 解:∵an=nsin2$\frac{n}{2}$π-ncos2$\frac{n}{2}$π=-ncosnπ=(-1)n-1n,
∴S2014=(1-2)+(3-4)+…+(2013-2014)=-1007.
S2015=S2014+a2015=-1007+2015=1008.
∴S2014+S2015=1.
点评 本题考查了数列求和、“分组求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
18.在数列{an}中,a1=1,若an-an-1=n-1(n∈N*,n≥2),则数列{an}的通项公式an=( )
| A. | $\frac{n(n+1)}{2}$ | B. | $\frac{{n}^{2}-n+2}{2}$ | C. | 2n2-n | D. | 2n-1 |
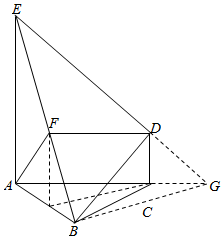 如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,且F为的BE中点
如图所示,△ABC是正三角形,线段EA和DC都垂直于平面ABC,设EA=AB=2a,且F为的BE中点