题目内容
已知A（-1，cosθ），B（sinθ，1），若|
+
|=|
-
|（O为坐标原点），则锐角θ= ．
| OA |
| OB |
| OA |
| OB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：|
+
|=|
-
|（O为坐标原点），可得：以OA，OB为邻边的平行四边形为矩形，于是
⊥
，利用
•
=-sinθ+cosθ=0，即可得出．
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
解答：
解：∵|
+
|=|
-
|（O为坐标原点），
∴以OA，OB为邻边的平行四边形为矩形，
∴
⊥
，
∴
•
=-sinθ+cosθ=0，θ为锐角．
∴tanθ=1，
解得θ=
．
故答案为：
．
| OA |
| OB |
| OA |
| OB |
∴以OA，OB为邻边的平行四边形为矩形，
∴
| OA |
| OB |
∴
| OA |
| OB |
∴tanθ=1，
解得θ=
| π |
| 4 |
故答案为：
| π |
| 4 |
点评：本题考查了向量的平行四边形法则、向量垂直与数量积的关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
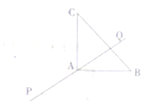如图，在Rt△ABC中，|