题目内容
7.定义在R上的函数f(x)满足f(x)+f(x+4)=16,当x∈(0,4]时,f(x)=x2-2x,则函数f(x)在[-4,2016]上的零点个数是( )| A. | 504 | B. | 505 | C. | 1008 | D. | 1009 |
分析 由f(x)+f(x+4)=16可判断出f(x)=f(x+8),从而可得函数f(x)是R上周期为8的函数;而当x∈(-4,4]时,f(2)=f(4)=0;从而解得.
解答 解:当x∈(-4,0]时,x+4∈(0,4],
f(x)=16-f(x+4)=16-((x+4)2-2x+4),
∵f(x)+f(x+4)=16,
∴f(x+4)+f(x+8)=16,
∴f(x)=f(x+8),
∴函数f(x)是R上周期为8的函数;
当x∈(-4,4]时,f(2)=f(4)=0;
而2020=8×252+4,
f(2)=f(10)=f(18)=…=f(8×251+2),
f(-4)=f(4)=f(8×251+4),
故函数f(x)在[-4,2016]上的零点个数是251+1+251+2=505,
故选B.
点评 本题考查了函数的性质的判断与应用,同时考查了归纳思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.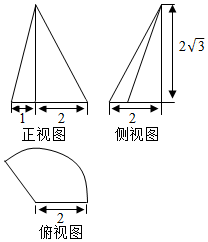 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
12.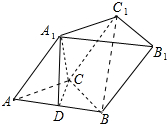 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
(1)求证:平面A1CD⊥平面A1AB;
(2)求二面角A1-BC-C1的余弦值.
 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.(1)求证:平面A1CD⊥平面A1AB;
(2)求二面角A1-BC-C1的余弦值.
17.空间9个点分布异面直线L1、L2上,L1上有4个点,L2上有5个点,则由它们可确定异面直线的对数为( )
| A. | 121对 | B. | 108对 | C. | 21对 | D. | 60对 |