题目内容
15.已知抛物线C1:y2=16x上的点P到圆C2:(x-4)2+y2=$\frac{32}{41}$的圆心的距离等于8,则抛物线C1在点P处的切线l1与C2经过点P的切线l2构成的角中,较小的角θ的正切值等于$\frac{4}{5}$.分析 求得圆的圆心和半径,抛物线的焦点和准线方程,运用抛物线的定义,求得P的坐标,对抛物线求导,可得切线l1的斜率,再由直线和圆相切的条件:d=r,求得切线l2的斜率,运用两直线的到角公式,计算即可得到所求最小值.
解答 解:圆C2:(x-4)2+y2=$\frac{32}{41}$的圆心为(4,0),半径为$\sqrt{\frac{32}{41}}$,
抛物线C1:y2=16x的焦点为(4,0),准线为x=-4,
由抛物线的定义可得xP+4=8,
解得xP=4,yP=±8,
取P(4,8),对抛物线y2=16x,两边对x求导,可得:
2yy′=16,即有切线l1的斜率为$\frac{8}{8}$=1,
由直线和圆相切的条件可得d=r,
设过P的切线方程为y-8=k(x-4),即为kx-y+8-4k=0,
即有$\frac{|8|}{\sqrt{1+{k}^{2}}}$=$\sqrt{\frac{32}{41}}$,解得k=±9,
由两直线的到角公式可得tanα=$\frac{9-1}{1+9}$=$\frac{4}{5}$,或tanβ=$\frac{-9-1}{1-9}$=$\frac{5}{4}$.
可得较小的角θ的正切值等于$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查抛物线的定义、方程和性质,注意运用焦点和准线方程,同时考查抛物线的切线和圆的切线方程,考查运算能力,属于中档题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
7.定义在R上的函数f(x)满足f(x)+f(x+4)=16,当x∈(0,4]时,f(x)=x2-2x,则函数f(x)在[-4,2016]上的零点个数是( )
| A. | 504 | B. | 505 | C. | 1008 | D. | 1009 |
4.直线x=1,x=2,y=0及曲线y=x3围成的平面图形的面积为( )
| A. | $\sum_{i=1}^{n}$$\frac{1}{n}$(1+$\frac{i}{n}$)3 | B. | ${∫}_{1}^{2}$x3dx | C. | ${∫}_{2}^{1}$x3dx | D. | 1 |
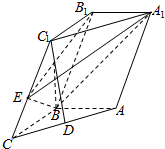 如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.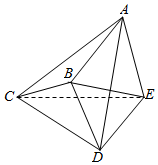 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD. 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{3π}{4}$.