题目内容
12.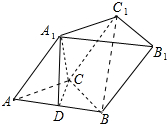 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.(1)求证:平面A1CD⊥平面A1AB;
(2)求二面角A1-BC-C1的余弦值.
分析 (1)根据面面垂直的判定定理即可证明平面A1CD⊥平面A1AB;
(2)建立坐标系,求出平面的法向量利用向量法即可求二面角A1-BC-C1的余弦值.
解答 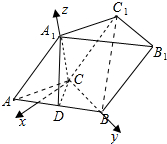 证明:(1)∵A1C⊥底面ABC,AB?平面,
证明:(1)∵A1C⊥底面ABC,AB?平面,
∴A1C⊥AB,
∵AC=BC=2,D为AB中点,
∴AB⊥CD,
∵CD∩A1C=C,
∴AB⊥平面A1CD,
∵AB?平面A1AB;
∴平面A1CD⊥平面A1AB;
(2)建立以C为坐标原点的空间直角坐标系如图:
∵∠ACB=120°,A1C=AC=BC=2,
∴C(0,0,0),B(0,2,0),A($\sqrt{3}$,-1,0),A1(0,0,2),
$\overrightarrow{CB}$=(0,2,0),$\overrightarrow{C{C}_{1}}$=$\overrightarrow{A{A}_{1}}$=(-$\sqrt{3}$,1,2),
$\overrightarrow{C{A}_{1}}$=(0,0,2),
设面A1BC的一个法向量为$\overrightarrow{m}$=(1,0,0).
设面BCC1的一个法向量为$\overrightarrow{n}$=(x,y,z)
则$\overrightarrow{n}$•$\overrightarrow{CB}$=2y=0,
$\overrightarrow{n}$•$\overrightarrow{C{C}_{1}}$=-$\sqrt{3}$x+y+2z=0,
则y=0,令z=$\sqrt{3}$,则x=2,
即$\overrightarrow{n}$=(2,0,$\sqrt{3}$),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2}{1×\sqrt{4+3}}=\frac{2}{\sqrt{7}}$=$\frac{2\sqrt{7}}{7}$,
即二面角A1-BC-C1的余弦值是$\frac{2\sqrt{7}}{7}$.
点评 本题主要考查面面垂直的判断以及利用空间向量求平面间的夹角.解决问题的关键在于先建立空间直角坐标系,求出各点的坐标,进而求出两个半平面的法向量.

| A. | 504 | B. | 505 | C. | 1008 | D. | 1009 |
| A. | $\sum_{i=1}^{n}$$\frac{1}{n}$(1+$\frac{i}{n}$)3 | B. | ${∫}_{1}^{2}$x3dx | C. | ${∫}_{2}^{1}$x3dx | D. | 1 |
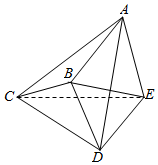 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.