题目内容
已知数列{bn}满足b1=
，a1=
，an+bn=1，bn+1=
．
（Ⅰ）求b1，b2，b3，b4；
（Ⅱ）求数列{ bn}的通项公式．
| 3 |
| 4 |
| 1 |
| 4 |
| bn | ||
1
|
（Ⅰ）求b1，b2，b3，b4；
（Ⅱ）求数列{ bn}的通项公式．
考点：数列递推式
专题：综合题,点列、递归数列与数学归纳法
分析：（Ⅰ）由an+bn=1，bn+1=
，可得bn+1=
，代入计算可求b2，b3，b4；
（Ⅱ）证明数列{
}是以-4为首项，-1为公差的等差数列，即可求数列{bn}的通项公式．
| bn | ||
1
|
| 1 |
| 2-bn |
（Ⅱ）证明数列{
| 1 |
| bn-1 |
解答：
解：（Ⅰ）∵an+bn=1，bn+1=
，
∴bn+1=
，
∵b1=
，a1=
，
∴b2=
，b3=
，b4=
；
（Ⅱ）∵bn+1=
，
∴bn+1-1=
-1，
∴
=-1+
，
∴数列{
}是以-4为首项，-1为公差的等差数列，
∴
=-4-（n-1）=-n-3，
∴bn=1-
=
．
| bn | ||
1
|
∴bn+1=
| 1 |
| 2-bn |
∵b1=
| 3 |
| 4 |
| 1 |
| 4 |
∴b2=
| 4 |
| 5 |
| 5 |
| 6 |
| 6 |
| 7 |
（Ⅱ）∵bn+1=
| 1 |
| 2-bn |
∴bn+1-1=
| 1 |
| 2-bn |
∴
| 1 |
| bn+1-1 |
| 1 |
| bn-1 |
∴数列{
| 1 |
| bn-1 |
∴
| 1 |
| bn-1 |
∴bn=1-
| 1 |
| n+3 |
| n+2 |
| n+3 |
点评：本题考查数列递推式，考查等差数列的证明，考查数列的通项，证明数列{
}是以-4为首项，-1为公差的等差数列是关键．
| 1 |
| bn-1 |
练习册系列答案
相关题目
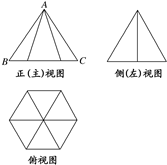一个几何体的三视图如图所示，其中正（主）视图中△ABC是边长为2的正三角形，俯视图的边界为正六边形，那么该几何体的侧）视图的面积为（ ）